11. 如图,点A,B,C,D,E,F均在$\odot O$上.若$∠ADF=20^{\circ },∠FEC=35^{\circ }$,则$∠ABC=$
55°
.
答案:
55°
12. 如图,$∠ABC=70^{\circ }$,O为射线BC上一点,以点O为圆心,$\frac {1}{2}OB$长为半径作圆.将射线BA绕点B顺时针旋转,使射线BA与$\odot O$相切,则旋转角的度数是______
40°或100°
.
答案:
40°或100°
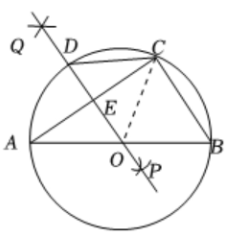
13. (10分)如图,AB是$\odot O$的直径,点C在$\odot O$上.尺规作图:过点O作AC的垂线,垂足为点E,交$\overset{\frown }{AC}$于点D,连接CD.(保留作图痕迹,不写作法)


答案:

14. (12分)[一题多解题]如图,A,B,C是$\odot O$上的三点,BO平分$∠ABC$.求证:$AB=BC$.


答案:
1. 证法一:
连接$OA$,$OC$。
因为$OA = OB$,$OB = OC$,所以$\angle OAB=\angle OBA$,$\angle OCB=\angle OBC$。
又因为$BO$平分$\angle ABC$,所以$\angle OBA=\angle OBC$。
则$\angle OAB=\angle OCB$。
在$\triangle OAB$和$\triangle OCB$中,$\left\{\begin{array}{l}OA = OC\\\angle OAB=\angle OCB\\OB = OB\end{array}\right.$。
根据$SAS$(边角边)定理,$\triangle OAB\cong\triangle OCB$。
所以$AB = BC$。
2. 证法二:
过点$O$作$OD\perp AB$于点$D$,$OE\perp BC$于点$E$。
因为$BO$平分$\angle ABC$,所以$OD = OE$。
又因为$OA = OC$,$OD\perp AB$,$OE\perp BC$。
根据垂径定理,$AB = 2AD$,$BC = 2CE$。
在$Rt\triangle OAD$和$Rt\triangle OCE$中,$\left\{\begin{array}{l}OA = OC\\OD = OE\end{array}\right.$。
根据$HL$(斜边直角边)定理,$Rt\triangle OAD\cong Rt\triangle OCE$。
所以$AD = CE$。
则$AB = BC$。
3. 证法三:
因为$BO$平分$\angle ABC$,所以$\angle ABO=\angle CBO$。
又因为$\angle AOB = 2\angle ACB$,$\angle COB = 2\angle CAB$(同弧所对的圆心角是圆周角的$2$倍)。
且$\angle ACB=\angle CAB$(等角对等弧)。
所以$\angle AOB=\angle COB$。
在$\triangle AOB$和$\triangle COB$中,$\left\{\begin{array}{l}OA = OC\\\angle AOB=\angle COB\\OB = OB\end{array}\right.$。
根据$SAS$(边角边)定理,$\triangle AOB\cong\triangle COB$。
所以$AB = BC$。
综上,$AB = BC$得证。
连接$OA$,$OC$。
因为$OA = OB$,$OB = OC$,所以$\angle OAB=\angle OBA$,$\angle OCB=\angle OBC$。
又因为$BO$平分$\angle ABC$,所以$\angle OBA=\angle OBC$。
则$\angle OAB=\angle OCB$。
在$\triangle OAB$和$\triangle OCB$中,$\left\{\begin{array}{l}OA = OC\\\angle OAB=\angle OCB\\OB = OB\end{array}\right.$。
根据$SAS$(边角边)定理,$\triangle OAB\cong\triangle OCB$。
所以$AB = BC$。
2. 证法二:
过点$O$作$OD\perp AB$于点$D$,$OE\perp BC$于点$E$。
因为$BO$平分$\angle ABC$,所以$OD = OE$。
又因为$OA = OC$,$OD\perp AB$,$OE\perp BC$。
根据垂径定理,$AB = 2AD$,$BC = 2CE$。
在$Rt\triangle OAD$和$Rt\triangle OCE$中,$\left\{\begin{array}{l}OA = OC\\OD = OE\end{array}\right.$。
根据$HL$(斜边直角边)定理,$Rt\triangle OAD\cong Rt\triangle OCE$。
所以$AD = CE$。
则$AB = BC$。
3. 证法三:
因为$BO$平分$\angle ABC$,所以$\angle ABO=\angle CBO$。
又因为$\angle AOB = 2\angle ACB$,$\angle COB = 2\angle CAB$(同弧所对的圆心角是圆周角的$2$倍)。
且$\angle ACB=\angle CAB$(等角对等弧)。
所以$\angle AOB=\angle COB$。
在$\triangle AOB$和$\triangle COB$中,$\left\{\begin{array}{l}OA = OC\\\angle AOB=\angle COB\\OB = OB\end{array}\right.$。
根据$SAS$(边角边)定理,$\triangle AOB\cong\triangle COB$。
所以$AB = BC$。
综上,$AB = BC$得证。
15. (12分)如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的几何示意图,其中拱门最下端$AB=18dm$,C为AB的中点,D为拱门最高点,圆心O在线段CD上,$CD=27dm$,求拱门所在圆的半径.




答案:
解:拱门所在圆的半径是15 dm.
16. (14分)如图,以四边形ABCD的对角线BD为直径作圆,圆心为点O,过点A作$AE⊥CD$交CD的延长线于点E,且DA平分$∠BDE$.
(1)求证:AE是$\odot O$的切线;
(2)若$AE=4,CD=6$,求$\odot O$的半径和AD的长.

(1)求证:AE是$\odot O$的切线;
(2)若$AE=4,CD=6$,求$\odot O$的半径和AD的长.

答案:
1. (1)**证明$AE$是$\odot O$的切线**:
连接$OA$。
因为$OA = OD$,所以$\angle ODA=\angle OAD$。
又因为$DA$平分$\angle BDE$,所以$\angle ODA=\angle EDA$。
则$\angle OAD=\angle EDA$,所以$OA// DE$。
已知$AE\perp CD$,即$\angle AED = 90^{\circ}$,那么$\angle OAE=\angle AED = 90^{\circ}$(两直线平行,内错角相等)。
因为$OA$是$\odot O$的半径,且$OA\perp AE$,所以$AE$是$\odot O$的切线。
2. (2)**求$\odot O$的半径和$AD$的长**:
过点$O$作$OF\perp CD$于点$F$。
因为$OF\perp CD$,根据垂径定理,$DF=\frac{1}{2}CD$(垂直于弦的直径平分弦),已知$CD = 6$,所以$DF = 3$。
由(1)知$\angle OAE=\angle AED=\angle OFD = 90^{\circ}$,所以四边形$AOFE$是矩形。
则$OA=EF$,$AE = OF = 4$。
设$\odot O$的半径为$r$,则$OD=r$,$OA = r$,$EF=r$,$DE=r - 3$。
在$Rt\triangle ODF$中,根据勾股定理$OD^{2}=OF^{2}+DF^{2}$,即$r^{2}=4^{2}+3^{2}$。
解$r^{2}=16 + 9=25$,得$r = 5$($r=-5$舍去)。
因为$DE=r - 3=5 - 3 = 2$。
在$Rt\triangle ADE$中,根据勾股定理$AD=\sqrt{AE^{2}+DE^{2}}$。
已知$AE = 4$,$DE = 2$,所以$AD=\sqrt{4^{2}+2^{2}}=\sqrt{16 + 4}=\sqrt{20}=2\sqrt{5}$。
综上,(1)证明如上;(2)$\odot O$的半径为$5$,$AD$的长为$2\sqrt{5}$。
连接$OA$。
因为$OA = OD$,所以$\angle ODA=\angle OAD$。
又因为$DA$平分$\angle BDE$,所以$\angle ODA=\angle EDA$。
则$\angle OAD=\angle EDA$,所以$OA// DE$。
已知$AE\perp CD$,即$\angle AED = 90^{\circ}$,那么$\angle OAE=\angle AED = 90^{\circ}$(两直线平行,内错角相等)。
因为$OA$是$\odot O$的半径,且$OA\perp AE$,所以$AE$是$\odot O$的切线。
2. (2)**求$\odot O$的半径和$AD$的长**:
过点$O$作$OF\perp CD$于点$F$。
因为$OF\perp CD$,根据垂径定理,$DF=\frac{1}{2}CD$(垂直于弦的直径平分弦),已知$CD = 6$,所以$DF = 3$。
由(1)知$\angle OAE=\angle AED=\angle OFD = 90^{\circ}$,所以四边形$AOFE$是矩形。
则$OA=EF$,$AE = OF = 4$。
设$\odot O$的半径为$r$,则$OD=r$,$OA = r$,$EF=r$,$DE=r - 3$。
在$Rt\triangle ODF$中,根据勾股定理$OD^{2}=OF^{2}+DF^{2}$,即$r^{2}=4^{2}+3^{2}$。
解$r^{2}=16 + 9=25$,得$r = 5$($r=-5$舍去)。
因为$DE=r - 3=5 - 3 = 2$。
在$Rt\triangle ADE$中,根据勾股定理$AD=\sqrt{AE^{2}+DE^{2}}$。
已知$AE = 4$,$DE = 2$,所以$AD=\sqrt{4^{2}+2^{2}}=\sqrt{16 + 4}=\sqrt{20}=2\sqrt{5}$。
综上,(1)证明如上;(2)$\odot O$的半径为$5$,$AD$的长为$2\sqrt{5}$。
查看更多完整答案,请扫码查看


