22. (2024·蓬江区校级月考)【阅读材料】方程 $ ( x ^ { 2 } - 1 ) ^ { 2 } - 5 ( x ^ { 2 } - 1 ) + 4 = 0 $ 是一个一元四次方程,我们可以把 $ x ^ { 2 } - 1 $ 看成一个整体,设 $ x ^ { 2 } - 1 = y $,则原方程可化为 $ y ^ { 2 } - 5 y + 4 = 0 \cdots $①
解方程①可得 $ y _ { 1 } = 1, y _ { 2 } = 4 $.
当 $ y = 1 $ 时,$ x ^ { 2 } - 1 = 1, \therefore x ^ { 2 } = 2. \therefore x = \pm \sqrt { 2 } $;
当 $ y = 4 $ 时,$ x ^ { 2 } - 1 = 4, \therefore x ^ { 2 } = 5. \therefore x = \pm \sqrt { 5 } $.
$ \therefore $ 原方程的解为 $ x _ { 1 } = \sqrt { 2 }, x _ { 2 } = - \sqrt { 2 }, x _ { 3 } = \sqrt { 5 }, x _ { 4 } = - \sqrt { 5 } $.
【解决问题】(1)在由原方程到方程①的过程中,是利用换元法达到
(2)请仿照材料的方法,解下列方程:
①$ x ^ { 4 } - x ^ { 2 } - 6 = 0 $;
②$ ( x ^ { 2 } - x ) ^ { 2 } - 4 ( x ^ { 2 } - x ) - 12 = 0 $.
解方程①可得 $ y _ { 1 } = 1, y _ { 2 } = 4 $.
当 $ y = 1 $ 时,$ x ^ { 2 } - 1 = 1, \therefore x ^ { 2 } = 2. \therefore x = \pm \sqrt { 2 } $;
当 $ y = 4 $ 时,$ x ^ { 2 } - 1 = 4, \therefore x ^ { 2 } = 5. \therefore x = \pm \sqrt { 5 } $.
$ \therefore $ 原方程的解为 $ x _ { 1 } = \sqrt { 2 }, x _ { 2 } = - \sqrt { 2 }, x _ { 3 } = \sqrt { 5 }, x _ { 4 } = - \sqrt { 5 } $.
【解决问题】(1)在由原方程到方程①的过程中,是利用换元法达到
降次
的目的(填“降次”或“消元”),体现了数学的转化思想.(2)请仿照材料的方法,解下列方程:
①$ x ^ { 4 } - x ^ { 2 } - 6 = 0 $;
②$ ( x ^ { 2 } - x ) ^ { 2 } - 4 ( x ^ { 2 } - x ) - 12 = 0 $.
①设 $x^{2}=a$,则原方程可化为 $a^{2}-a - 6 = 0$。
解方程 $a^{2}-a - 6 = 0$,得 $a_{1}=3,a_{2}=-2$。
当 $a = 3$ 时,$x^{2}=3$,$\therefore x=\pm\sqrt{3}$;
当 $a = -2$ 时,$x^{2}=-2$,此方程无解。
$\therefore$ 原方程的解为 $x_{1}=\sqrt{3},x_{2}=-\sqrt{3}$。
②设 $x^{2}-x=y$,则原方程可化为 $y^{2}-4y - 12 = 0$。
解方程 $y^{2}-4y - 12 = 0$,得 $y_{1}=6,y_{2}=-2$。
当 $y = 6$ 时,$x^{2}-x=6$,$\therefore x_{1}=3,x_{2}=-2$;
当 $y = -2$ 时,$x^{2}-x=-2$,此方程无解。
$\therefore$ 原方程的解为 $x_{1}=3,x_{2}=-2$。
解方程 $a^{2}-a - 6 = 0$,得 $a_{1}=3,a_{2}=-2$。
当 $a = 3$ 时,$x^{2}=3$,$\therefore x=\pm\sqrt{3}$;
当 $a = -2$ 时,$x^{2}=-2$,此方程无解。
$\therefore$ 原方程的解为 $x_{1}=\sqrt{3},x_{2}=-\sqrt{3}$。
②设 $x^{2}-x=y$,则原方程可化为 $y^{2}-4y - 12 = 0$。
解方程 $y^{2}-4y - 12 = 0$,得 $y_{1}=6,y_{2}=-2$。
当 $y = 6$ 时,$x^{2}-x=6$,$\therefore x_{1}=3,x_{2}=-2$;
当 $y = -2$ 时,$x^{2}-x=-2$,此方程无解。
$\therefore$ 原方程的解为 $x_{1}=3,x_{2}=-2$。
答案:
解:
(1) 降次
(2) ①设 $x^{2}=a$,则原方程可化为 $a^{2}-a - 6 = 0$。
解方程 $a^{2}-a - 6 = 0$,得 $a_{1}=3,a_{2}=-2$。
当 $a = 3$ 时,$x^{2}=3$,$\therefore x=\pm\sqrt{3}$;
当 $a = -2$ 时,$x^{2}=-2$,此方程无解。
$\therefore$ 原方程的解为 $x_{1}=\sqrt{3},x_{2}=-\sqrt{3}$。
②设 $x^{2}-x=y$,则原方程可化为 $y^{2}-4y - 12 = 0$。
解方程 $y^{2}-4y - 12 = 0$,得 $y_{1}=6,y_{2}=-2$。
当 $y = 6$ 时,$x^{2}-x=6$,$\therefore x_{1}=3,x_{2}=-2$;
当 $y = -2$ 时,$x^{2}-x=-2$,此方程无解。
$\therefore$ 原方程的解为 $x_{1}=3,x_{2}=-2$。
(1) 降次
(2) ①设 $x^{2}=a$,则原方程可化为 $a^{2}-a - 6 = 0$。
解方程 $a^{2}-a - 6 = 0$,得 $a_{1}=3,a_{2}=-2$。
当 $a = 3$ 时,$x^{2}=3$,$\therefore x=\pm\sqrt{3}$;
当 $a = -2$ 时,$x^{2}=-2$,此方程无解。
$\therefore$ 原方程的解为 $x_{1}=\sqrt{3},x_{2}=-\sqrt{3}$。
②设 $x^{2}-x=y$,则原方程可化为 $y^{2}-4y - 12 = 0$。
解方程 $y^{2}-4y - 12 = 0$,得 $y_{1}=6,y_{2}=-2$。
当 $y = 6$ 时,$x^{2}-x=6$,$\therefore x_{1}=3,x_{2}=-2$;
当 $y = -2$ 时,$x^{2}-x=-2$,此方程无解。
$\therefore$ 原方程的解为 $x_{1}=3,x_{2}=-2$。
23. (2024·中山期中)综合与实践:阅读材料,并解答以下问题.
(1)【学习研究】我国数学家赵爽在其所著的《勾股圆方图注》中记录了关于一元二次方程的几何解法,以 $ x ^ { 2 } + 2 x - 35 = 0 $ 为例,求解过程如下:
①变形:将方程 $ x ^ { 2 } + 2 x - 35 = 0 $ 变形为 $ x ( x + 2 ) = 35 $;
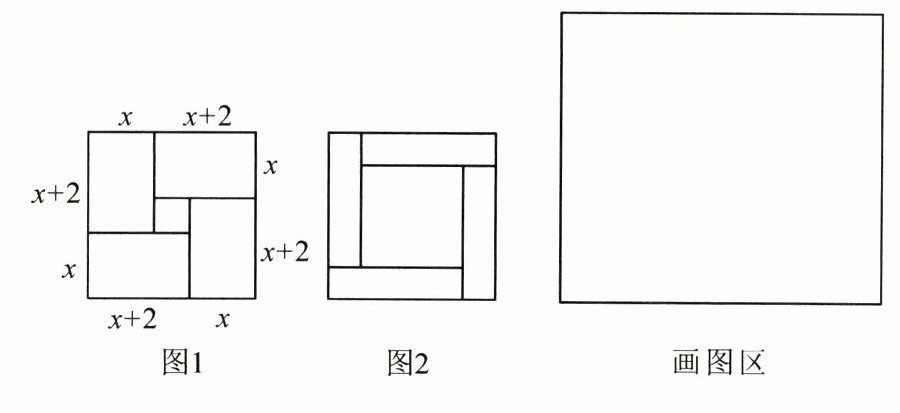
②构图:画四个长为 $ x + 2 $,宽为 $ x $ 的矩形,按如图1所示构造一个“空心”大正方形;
③解答:则图1中大正方形的面积从整体看可表示为 $ ( x + x + 2 ) ^ { 2 } $,从局部看还可表示为四个矩形与中间小正方形的面积之和,即 $ 4 x ( x + 2 ) + 2 ^ { 2 } = 4 × 35 + 4 = 144 $,因此,可得新的一元二次方程 $ ( x + x + 2 ) ^ { 2 } = 144. \because x $ 表示边长,$ \therefore 2 x + 2 = 12 $,即 $ x = 5 $.
这种数形结合的方法虽然只能得到原方程的其中一个正根,但是由新方程 $ ( x + x + 2 ) ^ { 2 } = 144 $ 可以得到原方程的另一个根是________.
(2)【类比迁移】根据赵爽几何解法的方法求解方程 $ x ^ { 2 } - 3 x - 4 = 0 $ 的一个正根.(写出完整的求解过程,并在画图区画出示意图,标明各边长)
(3)【拓展应用】一般地,对于形如 $ x ^ { 2 } + a x + b = 0 $ 的一元二次方程可以构造如图2所示的图形求解,已知图2是由四个面积为3的相同矩形构成,中间围成的正方形面积为4,那么 $ a = $________,$ b = $________,方程 $ x ^ { 2 } + a x + b = 0 $ 的一个正根为________.
(1)【学习研究】我国数学家赵爽在其所著的《勾股圆方图注》中记录了关于一元二次方程的几何解法,以 $ x ^ { 2 } + 2 x - 35 = 0 $ 为例,求解过程如下:
①变形:将方程 $ x ^ { 2 } + 2 x - 35 = 0 $ 变形为 $ x ( x + 2 ) = 35 $;
②构图:画四个长为 $ x + 2 $,宽为 $ x $ 的矩形,按如图1所示构造一个“空心”大正方形;
③解答:则图1中大正方形的面积从整体看可表示为 $ ( x + x + 2 ) ^ { 2 } $,从局部看还可表示为四个矩形与中间小正方形的面积之和,即 $ 4 x ( x + 2 ) + 2 ^ { 2 } = 4 × 35 + 4 = 144 $,因此,可得新的一元二次方程 $ ( x + x + 2 ) ^ { 2 } = 144. \because x $ 表示边长,$ \therefore 2 x + 2 = 12 $,即 $ x = 5 $.
这种数形结合的方法虽然只能得到原方程的其中一个正根,但是由新方程 $ ( x + x + 2 ) ^ { 2 } = 144 $ 可以得到原方程的另一个根是________.
(2)【类比迁移】根据赵爽几何解法的方法求解方程 $ x ^ { 2 } - 3 x - 4 = 0 $ 的一个正根.(写出完整的求解过程,并在画图区画出示意图,标明各边长)
(3)【拓展应用】一般地,对于形如 $ x ^ { 2 } + a x + b = 0 $ 的一元二次方程可以构造如图2所示的图形求解,已知图2是由四个面积为3的相同矩形构成,中间围成的正方形面积为4,那么 $ a = $________,$ b = $________,方程 $ x ^ { 2 } + a x + b = 0 $ 的一个正根为________.

答案:
解:
(1) $x = -7$
(2) 将方程 $x^{2}-3x - 4 = 0$ 变形为 $x(x - 3)=4$,画四个长为 $x$,宽为 $x - 3$ 的矩形,按如图 3 所示构造一个“空心”大正方形,

则图中大正方形的面积从整体看可表示为 $(x + x - 3)^{2}$,从局部看还可表示为四个矩形与中间小正方形的面积之和,即 $4x(x - 3)+3^{2}=4×4 + 9 = 25$,因此,可得新的一元二次方程 $(x + x - 3)^{2}=25$。
$\because x$ 表示边长,$\therefore 2x - 3 = 5$,即 $x = 4$。
(3) 2 -3 $x = 1$
解:
(1) $x = -7$
(2) 将方程 $x^{2}-3x - 4 = 0$ 变形为 $x(x - 3)=4$,画四个长为 $x$,宽为 $x - 3$ 的矩形,按如图 3 所示构造一个“空心”大正方形,

则图中大正方形的面积从整体看可表示为 $(x + x - 3)^{2}$,从局部看还可表示为四个矩形与中间小正方形的面积之和,即 $4x(x - 3)+3^{2}=4×4 + 9 = 25$,因此,可得新的一元二次方程 $(x + x - 3)^{2}=25$。
$\because x$ 表示边长,$\therefore 2x - 3 = 5$,即 $x = 4$。
(3) 2 -3 $x = 1$
查看更多完整答案,请扫码查看


