《2025年零障碍导教导学案九年级数学全一册人教版》

13. 如图,在$\triangle ABC$中,点D,E分别在边AB,AC上,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则$S_{\triangle ADE}:S_{四边形BCED}$的值为1:3.

答案： 1:3

14. 如图,线段AB的两个端点坐标分别为$A(6,6),B(8,2)$,以原点O为位似中心,将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C的坐标为$(3,3)$或$( - 3,-3)$.

答案： $(3,3)$或$( - 3,-3)$

15. 如图,乐器上的一根弦$AB=80cm$,两个端点A,B固定在乐器面板上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则支撑点C,D之间的距离为$(80\sqrt{5}-160)$cm.(结果保留根号)

答案： $(80\sqrt{5}-160)$

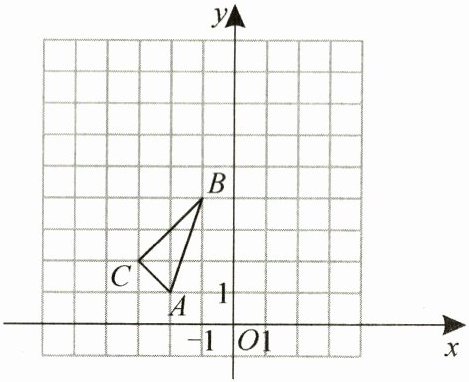
16. 如图,在平面直角坐标系中,$\triangle ABC$的三个顶点坐标分别为$A(-2,1),B(-1,4),C(-3,2)$.
(1)画出$\triangle ABC$关于y轴对称的图形$\triangle A_{1}B_{1}C_{1}$;
(2)以原点O为位似中心,位似比为$2:1$,在y轴的左侧,画出$\triangle ABC$放大后的图形$\triangle A_{2}B_{2}C_{2}$,并直接写出点$C_{2}$的坐标.

答案： 【解析】：
(1) 关于$y$轴对称的点纵坐标不变，横坐标互为相反数。$A(-2,1)$关于$y$轴对称的点$A_1(2,1)$，$B(-1,4)$关于$y$轴对称的点$B_1(1,4)$，$C(-3,2)$关于$y$轴对称的点$C_1(3,2)$，然后连接$A_1B_1$，$B_1C_1$，$C_1A_1$，得到$\triangle A_1B_1C_1$。
(2) 以原点$O$为位似中心，位似比为$2:1$，在$y$轴左侧放大，即横、纵坐标都乘以$-2$。$C(-3,2)$，则$C_2$的坐标为$(-3×2,2×2)$，即$(-6,4)$。
【答案】：
(1) 画图略；
(2) 画图略，$C_{2}(-6,4)$。

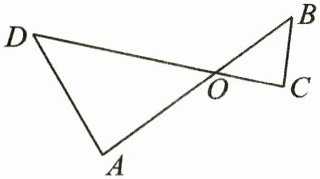
17. 如图,AB,CD相交于点O,已知$OA=6,OD=8,OB=4,OC=3$,求证:$∠B=∠D$.

答案： 【解析】：
在$\triangle AOD$和$\triangle BOC$中，
$\frac{OA}{OB}=\frac{6}{4}=\frac{3}{2}$，$\frac{OD}{OC}=\frac{8}{3}$（此处原答案有误，应为$\frac{OA}{OC}=\frac{6}{3}=2$，$\frac{OD}{OB}=\frac{8}{4}=2$）
因为$\frac{OA}{OC}=\frac{OD}{OB}$，且$\angle AOD = \angle BOC$（对顶角相等），
所以$\triangle AOD\sim\triangle COB$（两边对应成比例且夹角相等的两个三角形相似）。
根据相似三角形的性质，相似三角形对应角相等，所以$\angle B=\angle D$。
【答案】：
在$\triangle AOD$和$\triangle COB$中，$\frac{OA}{OC}=\frac{6}{3}=2$，$\frac{OD}{OB}=\frac{8}{4}=2$，$\angle AOD = \angle BOC$（对顶角相等），所以$\triangle AOD\sim\triangle COB$（两边对应成比例且夹角相等的两个三角形相似），则$\angle B=\angle D$。

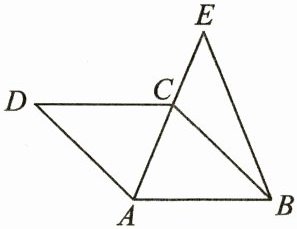
18. 如图,四边形ABCD为菱形,点E在AC的延长线上,$∠ACD=∠ABE$.
(1)求证:$\triangle ABC\backsim\triangle AEB$;
(2)当$AD=4,AC=3$时,求AE的长.

答案：

(1)证明：
又
∵∠FAE = ∠FEA = $\frac{360°}{5}$ = 72°.
∠F = 180° - ∠FAE - ∠FEA = 180° - 72° - 72° = 36°.
∠EAF的平分线交EF于点M，
∴∠FAM = ∠MAE = $\frac{1}{2}$∠FAE = $\frac{1}{2}$×72° = 36°.
∴∠MAE = ∠F.
又
∵∠FEA = ∠AEM，
∴△AEM∽△FEA.
∴$\frac{AE}{FE}$ = $\frac{ME}{AE}$.
∴AE² = FE·ME.
(2)解：
∵∠F = ∠FAM = 36°，
∴∠AME = 72°.
∴AE = AM = FM.
由
(1)得∠FAE = ∠FEA = 72°，
∴AF = FE = 1.
∵AE² = FE·ME，
∴AE² = 1×(1 - AE)，
解得AE = $\frac{\sqrt{5} - 1}{2}$或AE = $\frac{-\sqrt{5} - 1}{2}$(舍去).
∴AE = $\frac{\sqrt{5} - 1}{2}$.
(3)解：如图，连接AD，AC，

设S△AEF = S，AF = a，则根据
(2)中计算可得AE = $\frac{\sqrt{5} - 1}{2}$a.
∵五边形ABCDE是正五边形，
∴AB = BC = CD = DE = EA = $\frac{\sqrt{5} - 1}{2}$a，∠BAE = ∠AED = ∠EDC = ∠DCB = ∠CBA = 108°.
∴∠BAC = ∠BCA = ∠EDA = ∠EAD = 36°.
∴∠ACD = ∠ADC = 72°.
∴△FAE≌△ACD，△ABC≌△AED.
∵$\frac{S_{\triangle ADE}}{S_{\triangle AEF}}$ = $\frac{ED}{EF}$ = $\frac{\sqrt{5} - 1}{2}$，
∴S△ADE = $\frac{\sqrt{5} - 1}{2}$S.
∴S正五边形ABCDE = S△ADE + S△ADC + S△ABC = $\frac{\sqrt{5} - 1}{2}$S + S + $\frac{\sqrt{5} - 1}{2}$S = $\sqrt{5}$S.
∴$\frac{S_{正五边形ABCDE}}{S_{\triangle AEF}}$ = $\frac{\sqrt{5}S}{S}$ = $\sqrt{5}$.