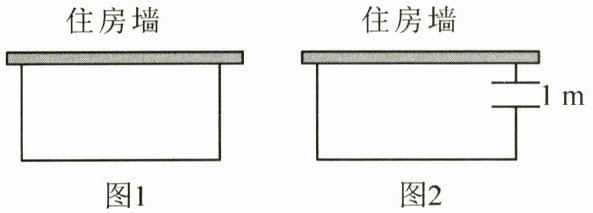
19. (2024·东莞校级月考)如图1,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成.
(1)要使所围矩形猪舍的面积达到 $ 50 m ^ { 2 } $,求猪舍的长和宽;
(2)农户想在现有材料的基础上扩建矩形猪舍,使其面积达到 $ 60 m ^ { 2 } $,小红为该农户提出了一个意见:“为方便进出,在垂直于住房墙的一边留一个1m宽的门就行.”如图2,请通过计算求小红设计的猪舍的长和宽.
(1)要使所围矩形猪舍的面积达到 $ 50 m ^ { 2 } $,求猪舍的长和宽;
(2)农户想在现有材料的基础上扩建矩形猪舍,使其面积达到 $ 60 m ^ { 2 } $,小红为该农户提出了一个意见:“为方便进出,在垂直于住房墙的一边留一个1m宽的门就行.”如图2,请通过计算求小红设计的猪舍的长和宽.

答案:
解:
(1) 设矩形猪舍垂直于墙的一边长为 $xm$,则平行于墙的一边长为 $(25 - 2x)m$,且 $25 - 2x\leqslant 12$,即 $x\geqslant 6.5$。
依题意,得 $x(25 - 2x)=50$,整理,得 $2x^{2}-25x + 50 = 0$,解得 $x_{1}=2.5$(不符合题意,舍去),$x_{2}=10$。
$\therefore 25 - 2x = 25 - 20 = 5$。
答:猪舍的长为 $10m$,宽为 $5m$。
(2) 设矩形猪舍垂直于墙的一边长为 $ym$,则平行于墙的一边长为 $(25 + 1 - 2y)m$,且 $25 + 1 - 2y\leqslant 12$,即 $y\geqslant 7$。
依题意,得 $y(25 + 1 - 2y)=60$,整理,得 $y^{2}-13y + 30 = 0$,解得 $y_{1}=3$(不符合题意,舍去),$y_{2}=10$。
$\therefore 26 - 2y = 26 - 20 = 6$。
答:小红设计的猪舍的长为 $10m$,宽为 $6m$。
(1) 设矩形猪舍垂直于墙的一边长为 $xm$,则平行于墙的一边长为 $(25 - 2x)m$,且 $25 - 2x\leqslant 12$,即 $x\geqslant 6.5$。
依题意,得 $x(25 - 2x)=50$,整理,得 $2x^{2}-25x + 50 = 0$,解得 $x_{1}=2.5$(不符合题意,舍去),$x_{2}=10$。
$\therefore 25 - 2x = 25 - 20 = 5$。
答:猪舍的长为 $10m$,宽为 $5m$。
(2) 设矩形猪舍垂直于墙的一边长为 $ym$,则平行于墙的一边长为 $(25 + 1 - 2y)m$,且 $25 + 1 - 2y\leqslant 12$,即 $y\geqslant 7$。
依题意,得 $y(25 + 1 - 2y)=60$,整理,得 $y^{2}-13y + 30 = 0$,解得 $y_{1}=3$(不符合题意,舍去),$y_{2}=10$。
$\therefore 26 - 2y = 26 - 20 = 6$。
答:小红设计的猪舍的长为 $10m$,宽为 $6m$。
20. (2024·东莞校级月考)已知关于 $ x $ 的一元二次方程 $ x ^ { 2 } - 2 x + m - 1 = 0 $ 有两个实数根.
(1)求 $ m $ 的取值范围;
(2)设 $ p $ 是方程的一个实数根,且满足 $ ( p ^ { 2 } - 2 p + 3 ) ( m + 4 ) = 7 $,求 $ m $ 的值.

(1)求 $ m $ 的取值范围;
(2)设 $ p $ 是方程的一个实数根,且满足 $ ( p ^ { 2 } - 2 p + 3 ) ( m + 4 ) = 7 $,求 $ m $ 的值.

答案:
解:
(1) $\because$ 关于 $x$ 的一元二次方程 $x^{2}-2x + m - 1 = 0$ 有两个实数根,$\therefore\Delta\geqslant 0$,即 $(-2)^{2}-4(m - 1)\geqslant 0$,解得 $m\leqslant 2$。
(2) $\because p$ 是方程的一个实数根,$\therefore p^{2}-2p + m - 1 = 0$。$\therefore p^{2}-2p = 1 - m$。
$\because (p^{2}-2p + 3)(m + 4)=7$,$\therefore (1 - m + 3)(m + 4)=7$,即 $m^{2}=9$,解得 $m = 3$ 或 $m = -3$。
又由
(1) 可知 $m\leqslant 2$,$\therefore m = -3$。
(1) $\because$ 关于 $x$ 的一元二次方程 $x^{2}-2x + m - 1 = 0$ 有两个实数根,$\therefore\Delta\geqslant 0$,即 $(-2)^{2}-4(m - 1)\geqslant 0$,解得 $m\leqslant 2$。
(2) $\because p$ 是方程的一个实数根,$\therefore p^{2}-2p + m - 1 = 0$。$\therefore p^{2}-2p = 1 - m$。
$\because (p^{2}-2p + 3)(m + 4)=7$,$\therefore (1 - m + 3)(m + 4)=7$,即 $m^{2}=9$,解得 $m = 3$ 或 $m = -3$。
又由
(1) 可知 $m\leqslant 2$,$\therefore m = -3$。
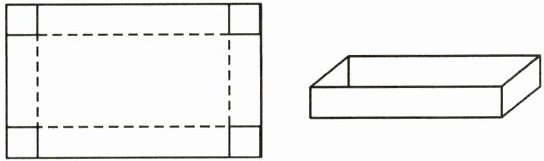
21. (2024·新会区校级月考)如图是一张长12dm、宽6dm的长方形纸板,将纸板四个角各剪去一个同样的边长为 $ x $ dm的正方形,然后将四周突出部分折起,可制成一个无盖长方体纸盒.
(1)无盖长方体纸盒盒底的长为
(2)若要制作一个底面积是 $ 40 d m ^ { 2 } $ 的无盖长方体纸盒,求剪去的正方形的边长 $ x $.
(1)无盖长方体纸盒盒底的长为
$12 - 2x$
dm,宽为$6 - 2x$
dm;(用含 $ x $ 的式子表示)(2)若要制作一个底面积是 $ 40 d m ^ { 2 } $ 的无盖长方体纸盒,求剪去的正方形的边长 $ x $.

解:(2)依题意,得 $(12 - 2x)(6 - 2x)=40$,整理,得 $x^{2}-9x + 8 = 0$,解得 $x_{1}=1,x_{2}=8$(不合题意,舍去)。
答:剪去的正方形的边长为 $1dm$。
答:剪去的正方形的边长为 $1dm$。
答案:
解:
(1) $(12 - 2x)(6 - 2x)$
(2) 依题意,得 $(12 - 2x)(6 - 2x)=40$,整理,得 $x^{2}-9x + 8 = 0$,解得 $x_{1}=1,x_{2}=8$(不合题意,舍去)。
答:剪去的正方形的边长为 $1dm$。
(1) $(12 - 2x)(6 - 2x)$
(2) 依题意,得 $(12 - 2x)(6 - 2x)=40$,整理,得 $x^{2}-9x + 8 = 0$,解得 $x_{1}=1,x_{2}=8$(不合题意,舍去)。
答:剪去的正方形的边长为 $1dm$。
查看更多完整答案,请扫码查看


