《2025年零障碍导教导学案九年级数学全一册人教版》

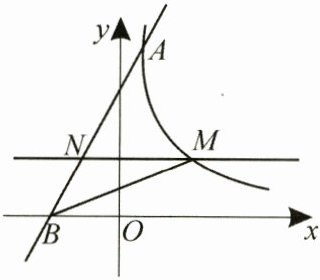
22. (2024·越秀区校级二模)如图,直线 $ y = 2x + 6 $ 与反比例函数 $ y = \frac{k}{x}(x ＞ 0) $ 的图象相交于点 $ A(1,m) $,与 $ x $ 轴相交于点 $ B $,直线 $ y = n(0 ＜ n ＜ 6) $ 交反比例函数的图象于点 $ M $,交 $ AB $ 于点 $ N $.
(1)直接写出:$ m $ 的值为______8,$ k $ 的值为______8.
(2)连接 $ BM $,当 $ n $ 为何值时,$ \triangle BMN $ 的面积最大?
依题意，得点$M$，$N$的坐标分别为$M(\frac{8}{n},n)$，$N(\frac{n - 6}{2},n)$，
$\because0 ＜ n ＜ 6$，$\therefore\frac{n - 6}{2}＜0$。
$\therefore S_{\triangle BMN}=\frac{1}{2}(|\frac{n - 6}{2}|+|\frac{8}{n}|)\cdot n$
$=-\frac{1}{4}(n - 3)^2+\frac{25}{4}$。
$\because-\frac{1}{4}＜0$，
$\therefore$当$n = 3$时，$\triangle BMN$的面积最大。
(3)当 $ \triangle BMN $ 的面积最大时,直接写出不等式 $ \frac{k}{x} ＞ n $ 的解集.$0 ＜ x ＜ \frac{8}{3}$

答案：
(1)8 8
(2)依题意，得点$M$，$N$的坐标分别为$M(\frac{8}{n},n)$，$N(\frac{n - 6}{2},n)$，
$\because0 ＜ n ＜ 6$，$\therefore\frac{n - 6}{2}＜0$。
$\therefore S_{\triangle BMN}=\frac{1}{2}(|\frac{n - 6}{2}|+|\frac{8}{n}|)\cdot n$
$=-\frac{1}{4}(n - 3)^2+\frac{25}{4}$。
$\because-\frac{1}{4}＜0$，
$\therefore$当$n = 3$时，$\triangle BMN$的面积最大。
(3)当$n = 3$时，$M(\frac{8}{3},3)$，
$\therefore$当$\triangle BMN$的面积最大时，不等式$\frac{k}{x}＞n$的解集为$0 ＜ x ＜ \frac{8}{3}$。

23. [中考新考法·数学跨学科探究与应用]【背景】在一次物理实验中,小冉同学用一固定电压为 $ 12 \text{ V} $ 的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡 $ \text{L} $(灯丝的阻值 $ R_{\text{L}} = 2 \Omega $)亮度的实验(如图),已知串联电路中,电流与电阻 $ R,R_{\text{L}} $ 之间关系为 $ I = \frac{U}{R + R_{\text{L}}} $,通过实验得出如下数据:
| $ R/\Omega $ | … | 1 | $ a $ | 3 | 4 | 6 | … |
| --- | --- | --- | --- | --- | --- | --- | --- |
| $ I/\text{A} $ | … | 4 | 3 | 2.4 | 2 | $ b $ | … |
(1)$ a = $______,$ b = $______;
(2)【探究】根据以上实验,构建出函数 $ y = \frac{12}{x + 2}(x \geq 0) $,结合表格信息,探究函数 $ y = \frac{12}{x + 2}(x \geq 0) $ 的图象与性质.
①在平面直角坐标系中画出对应函数 $ y = \frac{12}{x + 2} $ 的图象;
②随着自变量 $ x $ 的不断增大,函数值 $ y $ 的变化趋势是______.
(3)【拓展】结合(2)中函数图象分析,当 $ x \geq 0 $ 时,$ \frac{12}{x + 2} \geq -\frac{3}{2}x + 6 $ 的解集为______.

答案：

(1)2 1.5
(2)①根据表格数据描点，在平面直角坐标系中画出对应函数$y=\frac{12}{x + 2}$的图象如图所示。

②如图所示，由函数图象知，当$x\geq2$或$x = 0$时，$\frac{12}{x + 2}\geq-\frac{3}{2}x + 6$，
即当$x\geq0$时，$\frac{12}{x + 2}\geq-\frac{3}{2}x + 6$的解集为$x\geq2$或$x = 0$。
故答案为$x\geq2$或$x = 0$。