12. (2024·莘县校级月考)如图,在$\triangle ABC$中,$∠B = 30^{\circ},∠C = 45^{\circ},AC = 2$,则$BC = $
$\sqrt{6}+\sqrt{2}$
.
答案:
$\sqrt{6}+\sqrt{2}$
13. 如图,$\odot O$是$\triangle ABC$的外接圆,$AD$是$\odot O$的直径,若$\odot O$的半径为$\frac{3}{2},AC = 2$,则$\sin B = $
$\frac{2}{3}$
.
答案:
$\frac{2}{3}$
14. (2024·越秀区一模)如图,衣架可以近似看成一个等腰$\triangle ABC$,其中$AB = AC,∠ABC = 27^{\circ},BC = 40cm$,则高$AD$约为______cm. (参考数据:$\sin 27^{\circ} \approx 0.45,\cos 27^{\circ} \approx 0.89,\tan 27^{\circ} \approx 0.51$)


10.2
答案:
10.2
15. 将$45^{\circ}$的$∠AOB$按如图所示的方式放置在一把刻度尺上,顶点$O$与尺下沿的端点重合,$OA$与尺下沿重合,$OB$与尺上沿的交点$B$在尺上的读数恰为2cm,若按相同的方式将$22.5^{\circ}$的$∠AOC$放置在该刻度尺上,则$OC$与尺上沿的交点$C$在尺上的读数为
$2 \sqrt{2}+2$
cm.
答案:
$2 \sqrt{2}+2$
16. 计算:$2\cos 45^{\circ} - \frac{3}{2}\tan 30^{\circ}\cos 30^{\circ} + \sin^{2}60^{\circ}$.
答案:
解: 原式 $=2 × \frac{\sqrt{2}}{2}-\frac{3}{2} × \frac{\sqrt{3}}{3} × \frac{\sqrt{3}}{2}+\left(\frac{\sqrt{3}}{2}\right)^2$
$=\sqrt{2}-\frac{3}{4}+\frac{3}{4}$
$=\sqrt{2}$.
$=\sqrt{2}-\frac{3}{4}+\frac{3}{4}$
$=\sqrt{2}$.
17. 如图,在$\triangle ABC$中,$∠C = 90^{\circ},AB = 4\sqrt{6},BC = 4\sqrt{3}$,解这个直角三角形.


答案:
解: 在 $\triangle A B C$ 中, $\angle C=90^{\circ}, A B=4 \sqrt{6}, B C=4 \sqrt{3}$,
$\therefore \sin A=\frac{B C}{A B}=\frac{4 \sqrt{3}}{4 \sqrt{6}}=\frac{\sqrt{2}}{2}$.
$\therefore \angle A=45^{\circ}$.
$\therefore \angle B=90^{\circ}-\angle A=45^{\circ}$.
$\therefore \angle A=\angle B=45^{\circ}$.
$\therefore A C=BC=4 \sqrt{3}$.
$\therefore \sin A=\frac{B C}{A B}=\frac{4 \sqrt{3}}{4 \sqrt{6}}=\frac{\sqrt{2}}{2}$.
$\therefore \angle A=45^{\circ}$.
$\therefore \angle B=90^{\circ}-\angle A=45^{\circ}$.
$\therefore \angle A=\angle B=45^{\circ}$.
$\therefore A C=BC=4 \sqrt{3}$.
18. 如图,厂房屋顶人字架(等腰三角形)的跨度$BC = 10m,∠B = 30^{\circ}$,求中柱$AD$($D$为底边中点)的长.


答案:
解: $\because \triangle A B C$ 为等腰三角形,
$\therefore A B=AC$.
又 $\because D$ 为 $B C$ 的中点, $\therefore A D \perp B C$.
则在 $\mathrm{Rt} \triangle A D B$ 中, $AD=BD\cdot\tan B=\frac{BC}{2}\cdot\tan 30^{\circ}=\frac{10}{2} × \frac{\sqrt{3}}{3}=\frac{5 \sqrt{3}}{3}(m)$.
$\therefore A B=AC$.
又 $\because D$ 为 $B C$ 的中点, $\therefore A D \perp B C$.
则在 $\mathrm{Rt} \triangle A D B$ 中, $AD=BD\cdot\tan B=\frac{BC}{2}\cdot\tan 30^{\circ}=\frac{10}{2} × \frac{\sqrt{3}}{3}=\frac{5 \sqrt{3}}{3}(m)$.
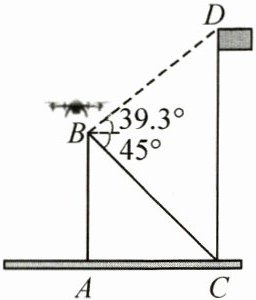
19. (2024·东莞一模)数学兴趣小组利用无人机测量旗杆的高度,在距离旗杆$CD$水平距离10m处,无人机垂直上升到$B$处,此时测得点$C$的俯角为$45^{\circ}$,点$D$的仰角为$39.3^{\circ}$,求旗杆$CD$的高度约为多少米. (结果保留整数,参考数据:$\sin 39.3^{\circ} \approx 0.63,\cos 39.3^{\circ} \approx 0.77,\tan 39.3^{\circ} \approx 0.82$)

答案:
解: 如图, 过点 $B$ 作 $B E \perp C D$, 垂足为 $E$,

依题意, 得 $BE=10m$.
在 $\mathrm{Rt} \triangle BCE$ 中, $\angle CBE=45^{\circ}$,
$\therefore CE=BE\cdot\tan 45^{\circ}=10(m)$.
在 $\mathrm{Rt} \triangle BDE$ 中, $\angle DBE=39.3^{\circ}$,
$\therefore DE=BE\cdot\tan 39.3^{\circ}\approx10×0.82 = 8.2(m)$.
$\therefore CD=DE + CE=8.2 + 10\approx18(m)$.
答: 旗杆 $CD$ 的高度约为 $18m$.
解: 如图, 过点 $B$ 作 $B E \perp C D$, 垂足为 $E$,

依题意, 得 $BE=10m$.
在 $\mathrm{Rt} \triangle BCE$ 中, $\angle CBE=45^{\circ}$,
$\therefore CE=BE\cdot\tan 45^{\circ}=10(m)$.
在 $\mathrm{Rt} \triangle BDE$ 中, $\angle DBE=39.3^{\circ}$,
$\therefore DE=BE\cdot\tan 39.3^{\circ}\approx10×0.82 = 8.2(m)$.
$\therefore CD=DE + CE=8.2 + 10\approx18(m)$.
答: 旗杆 $CD$ 的高度约为 $18m$.
查看更多完整答案,请扫码查看


