《2025年时习之暑假衔接八年级数学湘教版》

14. 若$\frac{a}{b}= \frac{3}{5}$,且$a+b= 24$,则$b-a= $______.

答案： 6

15. 如图,点$A$,$B的坐标分别为(1,2)$,$(4,0)$,将$\triangle AOB沿x$轴向右平移,得到$\triangle CDE$.已知$DB= 1$,则点$C$的坐标为______.

答案： $(4,2)$

16. 如图,在平面直角坐标系中,点$A在反比例函数y= \frac{k}{x}$($k$为常数,$k＞0$,$x＞0$)的图象上,过点$A作x$轴的垂线,垂足为$B$,连接$OA$.若$\triangle OAB$的面积为5,则$k= $______.

答案： 10

17. 如图,$\square ABCD的顶点B在矩形AEFC的边EF$上,点$B与点E$,$F$不重合.若$\triangle ACD$的面积为3,则图中阴影部分两个三角形的面积和为______.

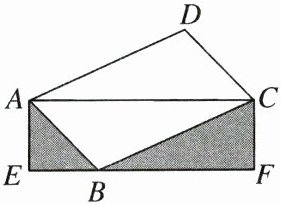
答案： 3

18. 如果三个数$a$,$b$,$c$满足其中一个数的两倍等于另外两个数的和,那么我们称这三个数$a$,$b$,$c$是“等差数”.若正比例函数$y= 2x的图象上有三点A(\frac{1}{2}m-1,y_{1})$,$B(m,y_{2})$,$C(2m+1,y_{3})$,且这三点的纵坐标$y_{1}$,$y_{2}$,$y_{3}$是“等差数”,则$m= $______.

答案： $-\frac{3}{2}$或0或$-\frac{6}{5}$解析：
∵正比例函数$y=2x$的图象上有三点$A(\frac{1}{2}m - 1,y_1)$，$B(m,y_2)$，$C(2m + 1,y_3)$，
∴$y_1 = m - 2$，$y_2 = 2m$，$y_3 = 4m + 2$。
∵$y_1$，$y_2$，$y_3$是“等差数”，
∴$2(m - 2) = 2m + 4m + 2$，或$4m = m - 2 + 4m + 2$，或$8m + 4 = m - 2 + 2m$。
∴$m = -\frac{3}{2}$或0或$-\frac{6}{5}$。

19. (6分)解方程：$x^{2}-5x+6= 0$.

答案： 解：
∵$x^2 - 5x + 6 = 0$，
∴$(x - 2)(x - 3) = 0$。则$x - 2 = 0$或$x - 3 = 0$，解得$x_1 = 2$，$x_2 = 3$。

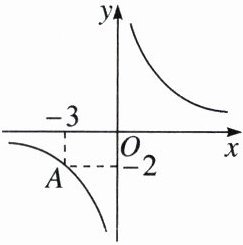
20. (6分)如图,已知反比例函数$y= \frac{k}{x}的图象经过点A(-3,-2)$.
(1)求反比例函数的表达式；
(2)若点$B(1,m)$,$C(3,n)$在该函数的图象上,试比较$m与n$的大小.

答案： 解：
(1)
∵反比例函数$y = \frac{k}{x}$的图象经过点$A(-3,-2)$，
∴$k = 6$。
∴反比例函数的表达式为$y = \frac{6}{x}$。
(2)
∵$k = 6 ＞ 0$，
∴图象在第一、三象限，$y$随$x$的增大而减小。又
∵$0 ＜ 1 ＜ 3$，
∴$B(1,m)$，$C(3,n)$两个点在第一象限。
∴$m ＞ n$。