《2025年时习之暑假衔接八年级数学湘教版》

26. (10分)如图,在正方形$ABCD$中,$AB= 3$,点$P为正方形ABCD的对角线AC$上一动点.

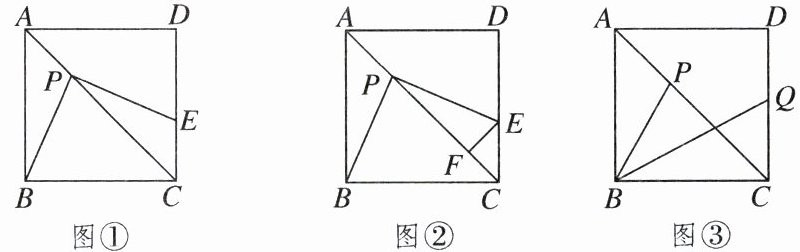
(1)如图①,过点$P作PE\perp PB交边DC于点E$.当点$E在边CD$上时,求证：$PB= PE$.
(2)如图②,在(1)的条件下,过点$E作EF\perp AC$,垂足为点$F$,在点$P$的运动过程中,$PF$的长度是否发生变化？若不变,求出这个不变的值；若变化,试说明理由.
(3)如图③,若点$Q是射线CD$上的一个动点,且始终满足$AP= CQ$,设$BP+BQ= t$,请直接写出$t^2$的最小值.

答案：
（1）证明：连接 $P D$。
∵四边形 $A B C D$ 是正方形，
∴ $C B = C D$，$ \angle P C B = \angle P C D = 45 ^ { \circ }$。在 $ \triangle P C B$ 和 $ \triangle P C D$ 中，$\begin{cases} C B = C D \\ \angle P C B = \angle P C D \\ C P = C P \end{cases}$，
∴ $ \triangle P C B \cong \triangle P C D ( S A S )$。
∴ $P B = P D$，$ \angle C B P = \angle C D P$。
∵ $P E \perp P B$，
∴ $ \angle B P E = \angle B C E = 90 ^ { \circ }$。
∴ $ \angle C B P + \angle C E P = 180 ^ { \circ }$。
∵ $ \angle C E P + \angle P E D = 180 ^ { \circ }$，
∴ $ \angle P E D = \angle C B P$。
∴ $ \angle P E D = \angle C D P$。
∴ $P E = P D$。
∴ $P B = P E$。
（2）解：$P F$ 的长度不变。连接 $B D$，与 $A C$ 相交于点 $O$。
∵四边形 $A B C D$ 是正方形，
∴ $ \angle B O P = 90 ^ { \circ }$。
∵ $P E \perp P B$，即 $ \angle B P E = 90 ^ { \circ }$，
∴ $ \angle P B O = 90 ^ { \circ } - \angle B P O = \angle E P F$。
∵ $E F \perp P C$，即 $ \angle P F E = 90 ^ { \circ }$，
∴ $ \angle B O P = \angle P F E$。在 $ \triangle B O P$ 和 $ \triangle P F E$ 中，$\begin{cases} \angle P B O = \angle E P F \\ \angle B O P = \angle P F E \\ P B = E P \end{cases}$，
∴ $ \triangle B O P \cong \triangle P F E ( A A S )$。
∴ $B O = P F$。
∵四边形 $A B C D$ 是正方形，
∴ $O B = O C$，$ \angle B O C = 90 ^ { \circ }$。
∴ $B C = \sqrt { 2 } O B$。
∵ $B C = A B = 3$，
∴ $O B = \frac { 3 \sqrt { 2 } } { 2 }$。
∴ $P F = O B = \frac { 3 \sqrt { 2 } } { 2 }$。
∴点 $P$ 在运动过程中，$P F$ 的长度不变，这个不变的值为 $ \frac { 3 \sqrt { 2 } } { 2 }$。
（3）$t ^ { 2 }$ 的最小值为 $18 + 9 \sqrt { 2 }$。解析：过点 $C$ 作 $C R \perp A C$，使 $C R = A B = 3$，连接 $Q R$，$B R$，过点 $R$ 作 $R T \perp B C$，交 $B C$ 的延长线于 $T$，如图③所示。
∵四边形 $A B C D$ 是正方形，
∴ $ \angle A C B = \angle A C D = \angle B A P = 45 ^ { \circ }$。
∵ $C R \perp A C$，
∴ $ \angle R C Q = 90 ^ { \circ } - 45 ^ { \circ } = 45 ^ { \circ }$，$ \angle R C T = 180 ^ { \circ } - 90 ^ { \circ } - 45 ^ { \circ } = 45 ^ { \circ }$。
∴ $ \triangle C T R$ 是等腰直角三角形，$ \angle B A P = \angle R C Q$。
∴ $C T = R T = \frac { \sqrt { 2 } } { 2 } C R = \frac { 3 \sqrt { 2 } } { 2 }$。
∴ $B T = B C + C T = 3 + \frac { 3 \sqrt { 2 } } { 2 }$。在 $ \triangle B A P$ 和 $ \triangle R C Q$ 中，$\begin{cases} A P = C Q \\ \angle B A P = \angle R C Q \\ A B = C R \end{cases}$，
∴ $ \triangle B A P \cong \triangle R C Q ( S A S )$。
∴ $B P = Q R$。
∴ $B$，$Q$，$R$ 三点共线时，$Q R + B Q$ 最短，即 $B P + B Q$ 最短，此时，$t = B R$。在 $ \mathrm { Rt } \triangle B T R$ 中，由勾股定理得 $B R ^ { 2 } = B T ^ { 2 } + R T ^ { 2 } = \left( 3 + \frac { 3 \sqrt { 2 } } { 2 } \right) ^ { 2 } + \left( \frac { 3 \sqrt { 2 } } { 2 } \right) ^ { 2 } = 18 + 9 \sqrt { 2 }$，
∴ $t ^ { 2 }$ 的最小值为 $18 + 9 \sqrt { 2 }$。