2025年时习之暑假衔接八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
24. (9分)为增强学生的身体素质,教育行政部门规定学生每天户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为0.5小时的人数,并补全条形统计图.
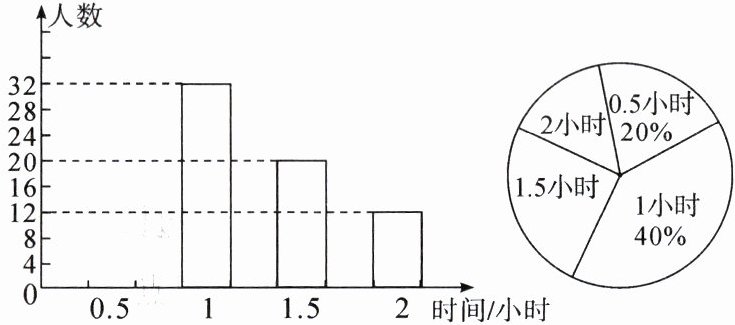
(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为0.5小时的人数,并补全条形统计图.

答案:
解:(1)$32 \div 40 \% = 80$(人)。故这次调查中共调查了 80 名学生。
(2)$80 \times 20 \% = 16$(人),故户外活动时间为 0.5 小时的有 16 人。补图略。
(2)$80 \times 20 \% = 16$(人),故户外活动时间为 0.5 小时的有 16 人。补图略。
25. (10分)【综合与实践】某学校在操场上举办“绑腿跑”比赛,要求每队若干名队员并列立于起跑线后,每相邻的两名队员把腿绑在一起,队员通过协调配合在跑道上共同行进.赛前某班队员在长方形比赛场地$ABCD$中(如图①所示)进行适应性训练,把这组“绑腿跑”队员表示为图中线段$MN$.线段$MN$可匀速向右或向左平行移动,该组“绑腿跑”队员从长方形$ABCD内平行于AB$边的某地出发向右匀速奔跑4s之后到达终点$CD$边,停留3s后又向左返回,匀速平行奔跑直至与$AB$边重合.
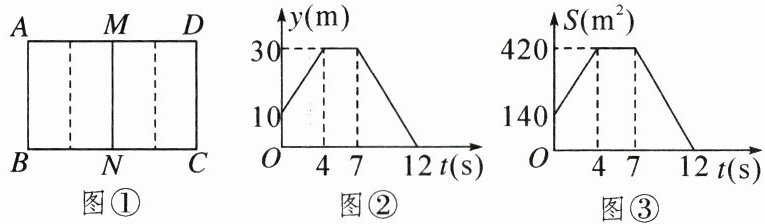
【问题分析】
(1)图②反映队员奔跑时与边$AB的距离y(m)$(即线段$BN$的长度)随时间$t(s)$变化而变化的情况.
①这个变化过程中,自变量是______,因变量是______;
②当这组队员开始出发时,到边$AB$的距离是______m;
③当$0<t\leqslant 4$时,求该“绑腿跑”队员向右运动的速度.
【实践探索】
(2)图③反映了队员在奔跑过程中形成长方形$ABNM的面积S(m^2)随时间t(s)$变化而变化的情况.
①长方形$ABCD中AB$边的长为______m;
②当$7\leqslant t\leqslant 12$时,请写出$S与y$之间的关系式.

【问题分析】
(1)图②反映队员奔跑时与边$AB的距离y(m)$(即线段$BN$的长度)随时间$t(s)$变化而变化的情况.
①这个变化过程中,自变量是______,因变量是______;
②当这组队员开始出发时,到边$AB$的距离是______m;
③当$0<t\leqslant 4$时,求该“绑腿跑”队员向右运动的速度.
【实践探索】
(2)图③反映了队员在奔跑过程中形成长方形$ABNM的面积S(m^2)随时间t(s)$变化而变化的情况.
①长方形$ABCD中AB$边的长为______m;
②当$7\leqslant t\leqslant 12$时,请写出$S与y$之间的关系式.
答案:
解:(1)①时间 $t$ 到边 $A B$ 的距离 $y$
② 10
③当 $0 < t \leq 4$ 时,该“绑腿跑”队员向右运动的速度为 $( 30 - 10 ) \div ( 4 - 0 ) = 5 ( \mathrm { m } / \mathrm { s } )$。
(2)① 14
②由题意可知,当 $7 \leq t \leq 12$ 时,$S$ 与 $y$ 之间的关系式为 $S = 14 y ( 0 \leq y \leq 30 )$。
② 10
③当 $0 < t \leq 4$ 时,该“绑腿跑”队员向右运动的速度为 $( 30 - 10 ) \div ( 4 - 0 ) = 5 ( \mathrm { m } / \mathrm { s } )$。
(2)① 14
②由题意可知,当 $7 \leq t \leq 12$ 时,$S$ 与 $y$ 之间的关系式为 $S = 14 y ( 0 \leq y \leq 30 )$。
查看更多完整答案,请扫码查看


