《2025年53精准练七年级数学下册北师大版山西专版》

13.如图,在△ABC中,分别以A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧交于M、N两点,作直线MN，交AB于点E，交AC于点D，若AE = 4，△BCD的周长是12，则△ABC的周长为__________.
　　

答案： 20

14.如图，射线OC是∠AOB的平分线，D为射线OC上一点，DP⊥OA于点P，PD = 3，若Q是射线OB上一点，OQ = 5，则阴影部分的面积为________.
　　

答案： $\frac{15}{2}$

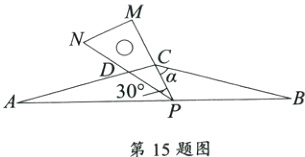
15.在△ABC中,CA = CB,∠ACB = 150°,将一把足够大的直角三角尺PMN (∠M = 90°，∠MPN = 30°)按如图所示放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角∠PCB = α,斜边PN 交AC于点D.在点P的滑动过程中,若△PCD是等腰三角形,则夹角α的度数为__________
　　

答案： 详解：因为∠ACB = 150°，∠PCB = α，
所以∠PCD = 150° - α，
①当PC = PD时，
∠PCD = ∠PDC = $\frac{180^{\circ}-30^{\circ}}{2}=75^{\circ}$，
即150° - α = 75°，
解得α = 75°；
②当PD = CD时，
∠PCD = ∠CPD = 30°，
即150° - α = 30°，
解得α = 120°；
③当PC = CD时，
∠CDP = ∠CPD = 30°，
所以∠PCD = 180° - 2×30° = 120°，
即150° - α = 120°，
解得α = 30°.
综上所述，当△PCD是等腰三角形时，α的度数为75°或120°或30°.

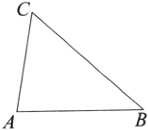
16.(6分)如图,在△ABC中,用尺规在△ABC内找一点D,使得直线CD平分△ABC的面积,且AD平分∠A.(不写作法，保留作图痕迹)
　

答案：
解：如图，点D即为所求.

17.(6分)如图,已知AC、DB的交点为E,AE = DE,∠A = ∠D,过点E作EF⊥BC,垂足为F.试说明:EF为△EBC的中线.
　

答案： 解：在△ABE和△DCE中，
$\begin{cases}\angle A=\angle D, \\AE = DE, \\\angle AEB=\angle DEC\end{cases}$
所以△ABE≌△DCE(ASA)，
所以EB = EC，
又因为EF⊥BC，
所以EF为△EBC的中线.