一 用棱长1cm的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色,数一数三面、两面、一面涂色以及没有涂色的小正方体各有多少块?

1. 观察4种涂色情况在正方体上的位置。完成下表。
|涂色的面|三面|两面|一面|没涂|
|----|----|----|----|----|
|2| | | | |
|3| | | | |
|4| | | | |
|5| | | | |
|...|...|...|...|...|
|12| | | | |
2. 我发现:
如果把一个棱长为$n(n\geqslant2)$的大正方体锯成棱长为1的小正方体,则:
(1)三面涂色的小正方体位于顶点处,每个顶点上有一块,共( )块。
(2)两面涂色的小正方体位于棱上,每条棱上有( )块,一共有( )块。
(3)一面涂色的小正方体位于面上,每个面中间有( )块,一共有( )块。
(4)没有涂色的小正方体位于大正方体内部,共有( )块。

1. 观察4种涂色情况在正方体上的位置。完成下表。
|涂色的面|三面|两面|一面|没涂|
|----|----|----|----|----|
|2| | | | |
|3| | | | |
|4| | | | |
|5| | | | |
|...|...|...|...|...|
|12| | | | |
2. 我发现:
如果把一个棱长为$n(n\geqslant2)$的大正方体锯成棱长为1的小正方体,则:
(1)三面涂色的小正方体位于顶点处,每个顶点上有一块,共( )块。
(2)两面涂色的小正方体位于棱上,每条棱上有( )块,一共有( )块。
(3)一面涂色的小正方体位于面上,每个面中间有( )块,一共有( )块。
(4)没有涂色的小正方体位于大正方体内部,共有( )块。
答案:
8@@0@@0@@0@@8@@12@@6@@1@@8@@24@@24@@8@@8@@36@@54@@27@@8@@120@@600@@1000@@8@@$n - 2$@@$12(n - 2)$@@$(n - 2)^2$@@$6(n - 2)^2$@@$(n - 2)^3$
二 从上往下数一数,下面图形中分别有多少个小正方体。
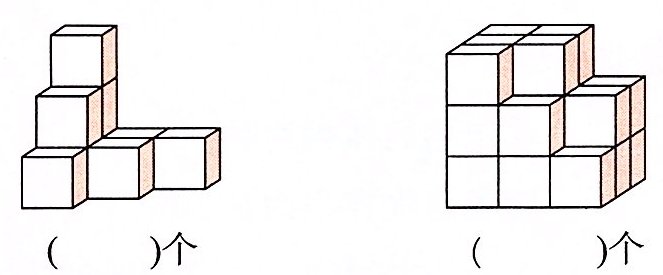

答案:
9@@22
三 若将这个几何体的表面涂上黄色(含底面)。只有1面涂色的有( )个小正方体;2面涂色的有( )个小正方体;3面涂色的有( )个小正方体;4面涂色的有( )个小正方体;5面涂色的有( )个小正方体。
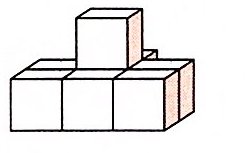

答案:
1@@0@@1@@4@@2
四 一个长方体木块,长是5dm,宽是4dm,高是3dm,先在它的六个面上都涂上色,然后把它锯成棱长都是1dm的小正方体木块(如图)。在锯成的小正方体木块中,三面涂色的有多少块?两面、一面涂色的各有多少块?六个面都没有涂色的有多少块?


答案:
三面:8块
两面:$(5 - 2)\times4+(4 - 2)\times4+(3 - 2)\times4 = 24$(块)
一面:$[(5 - 2)\times(4 - 2)+(5 - 2)\times(3 - 2)+(4 - 2)\times(3 - 2)]\times2 = 22$(块)
没涂色:$(5 - 2)\times(4 - 2)\times(3 - 2)=6$(块)
答:三面涂色的有8块,两面涂色的有24块,一面涂色的有22块,没涂色的有6块。
查看更多完整答案,请扫码查看


