《2025年小学学霸作业本四年级数学下册人教版广东专版》

1. 如图，在三角形ABC中，BC边上的高是线段(　　　)，AB边上的高是线段(　　　)。

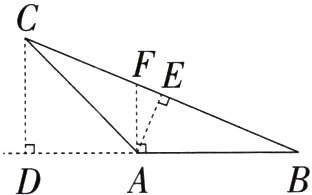
答案： AE CD

(1)已知一个三角形的两条边分别是15 cm和10 cm，第三条边可能是(　　　)。
A. 4 cm
B. 20 cm
C. 25 cm
D. 40 cm

答案：
(1)B

(2)有四根小棒，它们的长度分别是2 cm、3 cm、4 cm和5 cm，选择其中的三根围成三角形，能围出(　　　)个不同的三角形。
A. 1
B. 2
C. 3
D. 4

答案：
(2)C

3. 王老师准备了一根20 cm长的铁丝，用来做一个三角形框架。小明说：“如果用这根铁丝围成一个三角形，那么这个三角形的任何一条边都小于10 cm。”小明说得对吗？请写出小明的思考过程。

答案： 小明说得对。如果三角形中有一条边等于10 cm，20 - 10 = 10(cm)，则另外两条边的长度和是10 cm，不满足三角形的三边关系；如果三角形中有一条边大于10 cm，则另外两条边的长度和小于10 cm，也不满足三角形的三边关系。

4. 如图，三角形ABC是等边三角形，已知∠1 = 25°，∠2是多少度？

答案： $180^{\circ}\div3 = 60^{\circ}$ $180^{\circ}-60^{\circ}=120^{\circ}$
$\angle2 = 180^{\circ}-120^{\circ}-\angle1 = 35^{\circ}$
答：$\angle2$是$35^{\circ}$。

5. 如图，在三角形ABC和三角形ADE中标记了5个角，如果∠2 = ∠4，那么∠3与∠5是否相等？请说明你的理由。

答案： $\angle3$与$\angle5$相等。理由：在三角形ADE中，$\angle3 = 180^{\circ}-\angle1-\angle2$，在三角形ABC中，$\angle5 = 180^{\circ}-\angle1-\angle4$，$\angle2=\angle4$，$\angle1$是共同的角，所以$\angle3$与$\angle5$相等。