《2024年学习与评价江苏凤凰教育出版社七年级数学上册苏科版》

在现实世界中,我们看到的许多物体可以抽象为几何图形(几何体与平面图形).请你举例说说,哪些物体可以抽象出我们熟悉的几何图形(几何体与平面图形).

答案： ​​解:纸盒:长方体,足球:球等等。​​

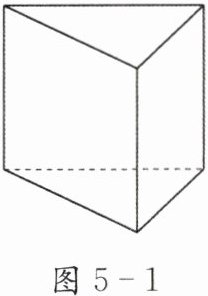
例1 如图5-1,用简洁的数学语言准确描述三棱柱的形状.
分析 描述几何体的构成,可以从面、线、点的形状、大小和数量关系等角度考虑.

答案： ​​ 解:5个面,6个顶点,底面是三角形且互相平行,侧面有3个,都是平行四边形。​​

例2 如图5-2,将下列几何体分类,并说明理由.
①
②
③
④
⑤

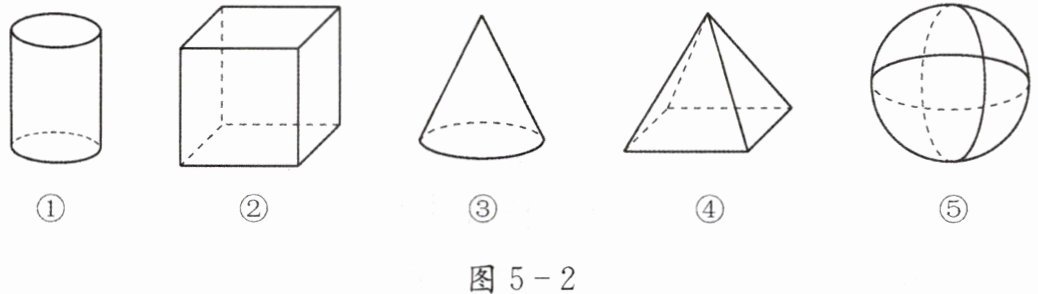
分析 分类标准可以不同,尝试多种分类标准,带来不同的分类方式.

答案： ​解:按柱体、锥体、球体将几何体分类如 下:柱体有①②,锥体有③④.球体有⑤.​
​按几何体的表面是平面和曲面分类如下:有曲面的几何体有①③⑤.无曲面的几何体有②④.​
​按有无顶点分类如下:有顶点的几何体有②③④,无顶点的几何体有①⑤.​

1. 在方框中画出下列各实物图抽象出的平面直观图,并在横线上写出该图形的名称.


□□□□□______ ______ ______ ______ ______

答案：





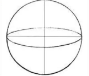
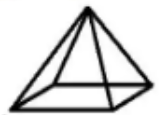
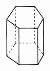
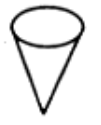
球
圆柱
四棱锥
六棱柱
圆锥