45.(丁中)过点(1,3)作直线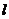 ,若
,若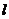 经过点
经过点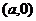 和
和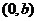 ,且
,且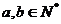 ,则可作出的
,则可作出的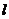 的条数为( )
的条数为( )
A. 1 B. 2 C. 3 D. 多于3
错解: D.
错因:忽视条件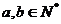 ,认为过一点可以作无数条直线.
,认为过一点可以作无数条直线.
正解: B.
44.(江安中学)直线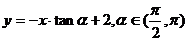 的倾斜角是(
)。
的倾斜角是(
)。
A. 
B.
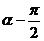
C.
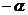
D. 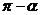
正解:D。由题意得:κ=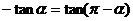
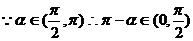
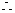 在[0,π]内正切值为κ的角唯一
在[0,π]内正切值为κ的角唯一
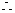 倾斜角为
倾斜角为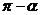
误解:倾斜角与题中显示的角 混为一谈。
混为一谈。
43.(江安中学)过点A(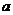 ,0)作椭圆
,0)作椭圆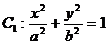 的弦,弦中点的轨迹仍是椭圆,记为
的弦,弦中点的轨迹仍是椭圆,记为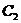 ,若
,若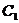 和
和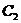 的离心率分别为
的离心率分别为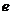 和
和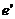 ,则
,则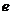 和
和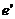 的关系是(
)。
的关系是(
)。
A. 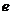 =
=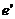
B.
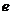 =2
=2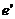
C.
2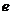 =
=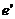
D. 不能确定
正解:A。设弦AB中点P(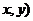 ,则B(
,则B(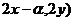
由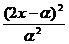 +
+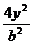 =1,
=1,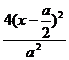 +
+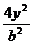 =1*
=1*
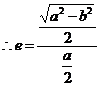 =
=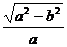
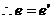
误解:容易产生错解往往在*式中前一式分子不从括号里提取4,而导致错误。
42.(江安中学)过抛物线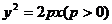 的焦点作一条直线交抛物线于
的焦点作一条直线交抛物线于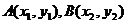 ,则
,则 为(
)
为(
)
A. 4
B. -4
C.
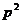
D. 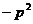
正解:D。 特例法:当直线垂直于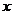 轴时,
轴时,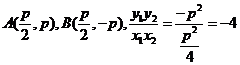
注意:先分别求出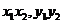 用推理的方法,既繁且容易出错。
用推理的方法,既繁且容易出错。
41.(江安中学)已知对称轴为坐标轴的双曲线的渐近线方程为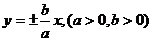 ,若双曲线上有一点M(
,若双曲线上有一点M(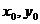 ),使
),使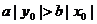 ,那双曲线的交点(
)。
,那双曲线的交点(
)。
A. 在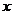 轴上
轴上
B.
在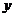 轴上
轴上
C.
当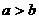 时在
时在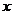 轴上
轴上
D. 当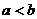 时在
时在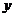 轴上
轴上
正解:B。 由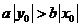 得
得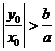 ,可设
,可设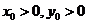 ,此时
,此时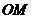 的斜率大于渐近线的斜率,由图像的性质,可知焦点在
的斜率大于渐近线的斜率,由图像的性质,可知焦点在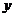 轴上。所以选B。
轴上。所以选B。
误解:设双曲线方程为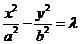 ,化简得:
,化简得: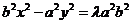 ,
,
代入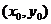 ,
,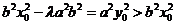 ,
,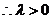 ,
,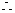 焦点在
焦点在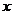 轴上。这个方法没错,但
轴上。这个方法没错,但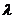 确定有误,应
确定有误,应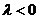 ,
,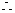 焦点在
焦点在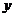 轴上。
轴上。
误解:选B,没有分组。
40.(江安中学)一条光线从点M(5,3)射出,与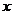 轴的正方向成
轴的正方向成 角,遇
角,遇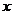 轴后反射,若
轴后反射,若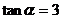 ,则反射光线所在的直线方程为(
)
,则反射光线所在的直线方程为(
)
A. 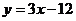
B.
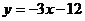
C.
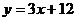
D. 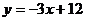
正解:D。 直线MN;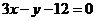 ,
,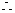 与
与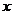 轴交点
轴交点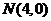 ,反射光线方程为
,反射光线方程为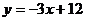 ,选D。
,选D。
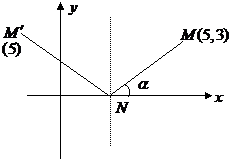

误解:反射光线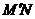 的斜率计算错误,得
的斜率计算错误,得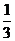 或
或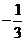 。
。
39.(江安中学)已知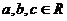 ,且
,且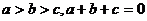 ,则下列判断正确的是( )
,则下列判断正确的是( )
A.
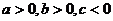
B.
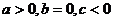
C.
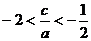
D.
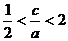
正解:C。
由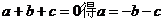 ①,又
①,又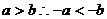 ②
②
由①②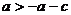
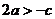 得
得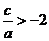
同理由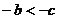 得
得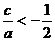 综上:
综上: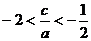
误解:D,不等式两边同乘-1时,不等号未变号。
38.(江安中学)已知直线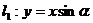 和直线
和直线 ,则直线
,则直线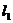 与
与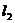 (
)。
(
)。
A. 通过平移可以重合
B. 不可能垂直
C.
可能与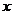 轴围成等腰直角三角形
轴围成等腰直角三角形
D.
通过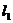 上某一点旋转可以重合
上某一点旋转可以重合
正解:D。
只要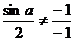 ,那么两直线就相交,若相交则可得到(D)。
,那么两直线就相交,若相交则可得到(D)。
误解:A,忽视了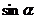 的有界性,误认为
的有界性,误认为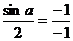
误解:B、C,忽视了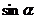 的有界性。
的有界性。
37.(江安中学)直线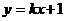 ,当
,当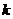 变化时,直线被椭圆
变化时,直线被椭圆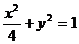 截得的最大弦长是(
)
截得的最大弦长是(
)
A. 4
B. 2
C.
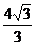
D. 不能确定
正解:C
直线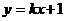 ,恒过P(0,1),又是椭圆的短轴上顶点,因而此直线被椭圆的弦长即为点P与椭圆上任意一点Q的距离,设椭圆上任意一点Q
,恒过P(0,1),又是椭圆的短轴上顶点,因而此直线被椭圆的弦长即为点P与椭圆上任意一点Q的距离,设椭圆上任意一点Q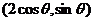 。
。
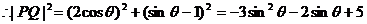
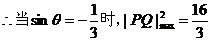
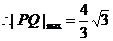 ,故选C
,故选C
误解:不能准确判断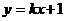 的特征:过P(0,1)。若用标准方程求解,计算容易出错。
的特征:过P(0,1)。若用标准方程求解,计算容易出错。
36.(江安中学)已知直线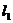 和
和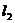 夹角的平分线为
夹角的平分线为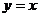 ,若
,若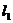 的方程是
的方程是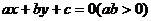 ,则
,则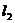 的方程是(
)。
的方程是(
)。
A. 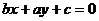
B.
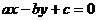
C.
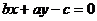
D. 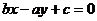
正解:A
法一: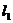 :
: ,而
,而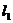 与
与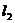 关于直线
关于直线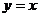 对称,则
对称,则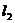 所表示的函数是
所表示的函数是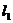 所表示的函数的反函数。
所表示的函数的反函数。
由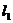 的方程得
的方程得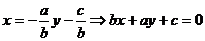 选A
选A
法二:找对称点(略)
误解:一般用找对称点法做,用这种方法有时同学不掌握或计算有误。

