9．(磨中)已知P是以F₁、F₂为焦点的双曲线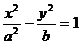上一点，PF₁⊥PF₂且tan∠PF₁F₂=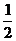，则此双曲线的离心率为_______________。

　 正确答案：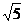

　 　错误原因：忽视双曲线定义的应用。

8．(磨中)双曲线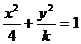的离心率为e，且e∈(1，2)则k的范围是________。

　 正确答案：k∈(-12，0)

　 错误原因：混淆了双曲线和椭圆的标准方程。

7．(磨中)过点(0，2)与抛物线y²=8x只有一个共点的直线有______条。

　 正确答案：3

　 错误原因：认为与抛物线只有一个共点的直线只能与抛物线相切而出错。

6．(磨中)已知双曲线的右准线为x=4，右焦点F(10，0)离心率e=2，则双曲线方程为______。

　 正确答案：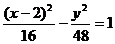

　 错误原因：误认为双曲线中心在原点，因此求出双曲线的标准方程而出现错误。

5．(磨中)过点(3，-3)且与圆(x-1)²+y²=4相切的直线方程是：___________。

　 正确答案：5x+12y+21=0或x=3

　 错误原因：遗漏了斜率不存在的情形造成漏解。

4．(磨中)已知直线l₁：x+y-2=0　 l₂：7x-y+4=0 则l₁与l₂夹角的平分线方程为______。

　 正确答案：6x+2y-3=0

　 错语原因：忽视两直线夹角的概念多求了夹角的邻补角的平分线方程。

3．(磨中)直线xCosx+y-1=0的倾斜角θ的取值范围为__________。

　 正确答案：θ∈[0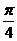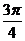，]∪[，π]

　 错误原因：由斜率范围求倾角范围在三角知识上出现错误；或忽视直线倾角的定义范围而得出其它错误答案。

2．(搬中)双曲线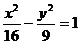上的点P到点(5,0)的距离为8.5，则点P到点(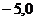)的距离_______。

　　 错解　 设双曲线的两个焦点分别为,,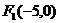

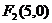　　 由双曲线定义知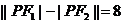

　　 所以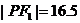或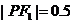

_{剖析　 由题意知，双曲线左支上的点到左焦点的最短距离为1,}

_{所以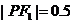不合题意，事实上，在求解此类问题时，应灵活运用双曲线定义，分析出点P的存在情况，然后再求解。如本题中，因左顶点到右焦点的距离为9>8.5，故点P只能在右支上，所求}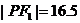

1．(如中)若直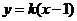线与抛物线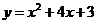的两个交点都在第二象，则k的取值范围是______________.　

解　　 答： (-3, 0)

易错原因：找不到确当的解答方法。本题最好用数形结合法。

56．(案中)过函数y=-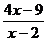的图象的对称中心，且和抛物线y²=8x有且只有一个公共点的直线的条数共有(　　 )

A、1条　　　　　 B、2条　　　 C、3条　　　　　　 D、不存在

正确答案：(B)

错误原因 ：解本题时极易忽视中心(2，4)在抛物线上，切线只有1条，又易忽视平行于抛物线对称轴的直线和抛物线只有一个公共点。

二填空题：