15.(石庄中学)已知 是三角形的一个内角,且sin
是三角形的一个内角,且sin +cos
+cos =
=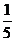 则方程x
则方程x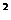 sin
sin -y
-y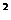 cos
cos =1表示( )
=1表示( )
A 焦点在x轴上的双曲线 B 焦点在y轴上的双曲线
C 焦点在x轴上的椭圆 D 焦点在y轴上的椭圆
正确答案:D 错因:学生不能由sin +cos
+cos =
=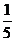 判断角
判断角 为钝角。
为钝角。
14.(石庄中学)双曲线 -
- =1中,被点P(2,1)平分的弦所在直线方程是( )
=1中,被点P(2,1)平分的弦所在直线方程是( )
A 8x-9y=7 B 8x+9y=25 C 4x-9y=16 D 不存在
正确答案:D 错因:学生用“点差法”求出直线方程没有用“△”验证直线的存在性。
13.(石庄中学)设双曲线 -
- =1与
=1与 -
- =1(a>0,b>0)的离心率分别为e
=1(a>0,b>0)的离心率分别为e 、e
、e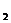 ,则当a、 b变化时,e
,则当a、 b变化时,e +e
+e 最小值是( )
最小值是( )
A 4 B 4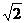 C
C 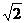 D 2
D 2
正确答案:A 错因:学生不能把e +e
+e 用a、
b的代数式表示,从而用基本不等式求最小值。
用a、
b的代数式表示,从而用基本不等式求最小值。
12.(石庄中学)平面上的动点P到定点F(1,0)的距离比P到y轴的距离大1,则动点P的轨迹方程为( )
A y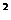 =2x
B y
=2x
B y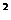 =2x 和
=2x 和 
C y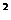 =4x
D y
=4x
D y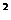 =4x 和
=4x 和 
正确答案:D 错因:学生只注意了抛物线的第二定义而疏忽了射线。
11.(石庄中学)在圆x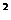 +y
+y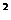 =5x内过点(
=5x内过点(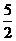 ,
,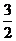 )有n条弦的长度成等差数列,最短弦长为数列首项a
)有n条弦的长度成等差数列,最短弦长为数列首项a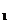 ,最长弦长为a
,最长弦长为a ,若公差d
,若公差d
 ,那么n的取值集合为( )
,那么n的取值集合为( )
A  B
B  C
C
 D
D

正确答案:A 错因:学生对圆内过点的弦何时最长、最短不清楚,不能借助d的范围来求n.
10.(石庄中学)已知圆
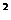 +y
+y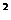 =4 和 直线y=mx的交点分别为P、Q两点,O为坐标原点, 则︱OP︱·︱OQ︱=( )
=4 和 直线y=mx的交点分别为P、Q两点,O为坐标原点, 则︱OP︱·︱OQ︱=( )
A 1+m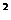 B
B 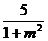 C 5
D 10
C 5
D 10
正确答案: C 错因:学生不能结合初中学过的切割线定︱OP︱·︱OQ︱等于切线长的平方来解题。
9.(石庄中学)P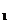 (x
(x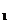 ,y
,y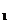 )是直线L:f(x,y)=0上的点,P
)是直线L:f(x,y)=0上的点,P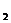 (x
(x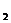 ,y
,y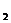 )是直线L外一点,则方程f(x,y)+f(x
)是直线L外一点,则方程f(x,y)+f(x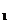 ,y
,y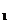 )+f(x
)+f(x 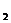 ,y
,y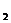 )=0所表示的直线(
)
)=0所表示的直线(
)
A 相交但不垂直 B 垂直 C 平行 D 重合
正确答案: C 错因:学生对该直线的解析式看不懂。
8.(石庄中学)能够使得圆x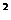 +y
+y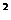 -2x+4y+1=0上恰好有两个点到直线2x+y+c=0距离等于1的一个值为( )
-2x+4y+1=0上恰好有两个点到直线2x+y+c=0距离等于1的一个值为( )
A 2
B 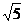 C 3
D 3
C 3
D 3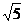
正确答案: C 错因:学生不能借助圆心到直线的距离来处理本题。
7.(石庄中学)P(-2,-2)、Q(0,-1)取一点R(2,m)使︱PR︱+︱RQ︱最小,则m=( )
A 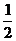 B 0 C
–1
D -
B 0 C
–1
D -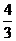
正确答案:D 错因:学生不能应用数形结合的思想方法,借助对称来解题。
6.(如中)若曲线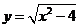 与直线
与直线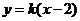 +3有两个不同的公共点,则实数 k 的取值范围是
+3有两个不同的公共点,则实数 k 的取值范围是
A 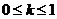 B
B 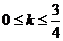 C
C 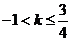 D
D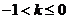
解 答:C
易错原因:将曲线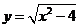 转化为
转化为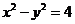 时不考虑纵坐标的范围;另外没有看清过点(2,-3)且与渐近线
时不考虑纵坐标的范围;另外没有看清过点(2,-3)且与渐近线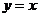 平行的直线与双曲线的位置关系。
平行的直线与双曲线的位置关系。

