20.(本题满分14分)某银行准备新设一种定期存款业务,经预测,存款量与存款利率成正比,比例系数为 ,贷款的利率为6%,又银行吸收的存款能全部放贷出去。
,贷款的利率为6%,又银行吸收的存款能全部放贷出去。
(1)若存款的利率为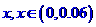 ,试分别写出存款数量
,试分别写出存款数量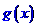 及银行应支付给储户的
及银行应支付给储户的
利息 与存款利率
与存款利率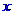 之间的关系式;
之间的关系式;
(2)存款利率定为多少时,银行可获得最大收益?
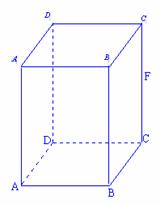
19.(本题满分14分)已知正四棱柱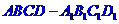 中,AB=2,
中,AB=2,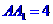 ,E为BC的中点,F为直线
,E为BC的中点,F为直线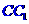
上动点。
(1)求异面直线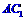 与
与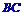 所成角的大小;
所成角的大小;
(2)(理)当F为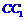 的中点时,求二面角
的中点时,求二面角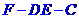 的大小
的大小
(文)当F为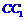 的中点时,求直线AF与平面
的中点时,求直线AF与平面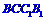 所成角的大小(用反三角函数表示);
所成角的大小(用反三角函数表示);
(3)证明:当点F在线段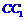 上移动时,三棱锥
上移动时,三棱锥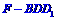 的体积是一个定值,并求出这个定值。
的体积是一个定值,并求出这个定值。
16.已知定义在区间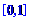 上的函数
上的函数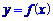 ,图象如右图所示,对满足
,图象如右图所示,对满足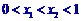 的任意
的任意
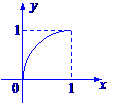
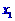 、
、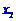 ,给出下列结论:①
,给出下列结论:① ;
;
②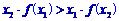 ;③
;③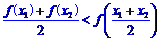 。其中正确
。其中正确
的结论有 ( )
|
(A)0个 |
(B)1个 |
(C)2个 |
(D)3个 |
14.已知直线l、m、n及平面a,下列命题中的假命题是 ( )
(A)若l//m,m//n,则l//n (B)若l⊥a,n//a,则l⊥n
(C)若l⊥m,m//n,则l⊥n (D)若l//a,n//a,则l//n
是符合题目要求的)
13.设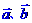 是两个非零向量,则“
是两个非零向量,则“ ”是“
”是“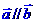 ”成立的( )
”成立的( )
(A)充要条件 (B)必要不充分条件.
(C)充分不必要条件. (D)既不充分也不必要条件
12.一水池有2个进水口,1个出水口,一个口进出水速度如图甲、乙所示.某天0点到6点,
该水池的蓄水量如图丙所示(至少打开一个水口),给出以下3个论断:
进水量 出水量 蓄水量
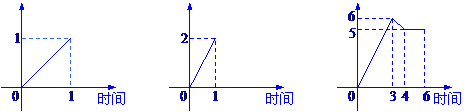
甲 乙 丙
(1)0点到3点只进水不出水;(2)3点到4点不进水只出水;(3)4点到6点不进水不
出水。则一定不确定的论断是 (把你认为是符合题意的论断序号都填上)。

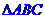 三个顶点分别是A(3,0)、B(0,3)、C
三个顶点分别是A(3,0)、B(0,3)、C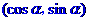 ,
,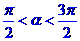 。
。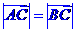 ,求角
,求角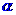 的值;
的值;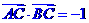 ,求
,求 的值。
的值。 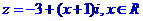 ,且
,且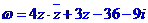 ,若
,若 表示的点在第四象限,求
表示的点在第四象限,求 的一个最大值点和一个最小值点,则r的取值范围是( )
的一个最大值点和一个最小值点,则r的取值范围是( )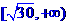 (B)
(B)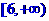 (C)
(C)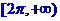 (D)以上都不对
(D)以上都不对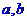 都是实数,给出下列条件:①
都是实数,给出下列条件:①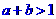 ;②
;②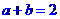 ;③
;③ ;
;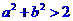 ;⑤
;⑤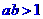 。其中能推出“
。其中能推出“ .(请
.(请