2.函数y = 2x3 –3x2 –12x + 5 在 [0 ,3 ] 上的最大值和最小值分别为 ( )
A.5 ,-15 B.5 ,-4 C.-4 ,-15 D.5 ,-16
22、(本小题满分14分)
(理)已知函数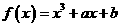 定义在区间
定义在区间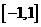 上,且
上,且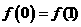 。又
。又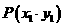 、
、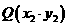 是其图像上任意两点
是其图像上任意两点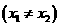 。
。
(1)
求证: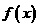 的图像关于点
的图像关于点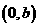 成中心对称图形;
成中心对称图形;
(2)
设直线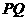 的斜率为
的斜率为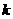 ,求证:
,求证: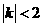 ;
;
(3)
若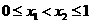 ,求证:
,求证: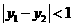 。
。
(文)已知函数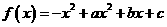 图像上的点
图像上的点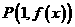 处的切线方程为
处的切线方程为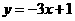 。
。
(1)
若函数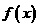 在
在 时有极值,求
时有极值,求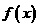 的表达式;
的表达式;
(2)
函数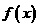 在区间
在区间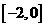 上单调递增,求实数
上单调递增,求实数 的取值范围。
的取值范围。
21、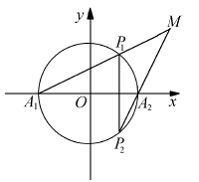 (本小题满分12分)
(本小题满分12分)
如图, 、
、 为圆
为圆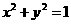 与
与 轴的两个交点,
轴的两个交点, 为垂直于
为垂直于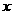 轴从弦,且
轴从弦,且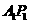 与
与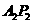 的交点为
的交点为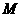 。
。
(1)
求动点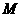 的轨迹方程;
的轨迹方程;
(2)
记动点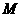 的轨迹为曲线
的轨迹为曲线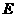 ,若过点
,若过点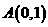 的直线
的直线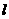 与曲线
与曲线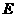 交于
交于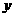 轴右边不同两点
轴右边不同两点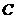 、
、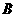 ,且
,且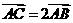 ,求直线
,求直线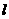 的方程。
的方程。
18、(本小题满分12分)
(理)一个口袋里有5个白球和3个黑球,任意取出一个,如果时黑球,则这个黑球不放回而另外放入一个白球,这样继续下去,直到取出的求时白球为止。求直到取到白球所需的抽取次数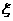 的概率分布列及
的概率分布列及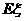 。
。
(文)在某次空战中,甲机先向乙机开火,击落乙机的概率时0.2;若乙机未被击落,就进行还击,击落甲机的概率时0.3;若甲机未被击落,则再进攻乙机,击落乙机的概率时0.4,求在这个三个回合中:
(1)甲机被击落的概率;
(2)乙机被击落的概率。
17、(本小题满分12分)
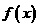 是定义在
是定义在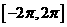 上的偶函数,当
上的偶函数,当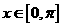 时,
时,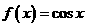 ,当
,当 时,
时,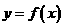 的图像时斜率为
的图像时斜率为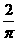 且在
且在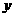 轴上的截距为
轴上的截距为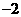 的直线在相应区间上的部分。
的直线在相应区间上的部分。
(1)
求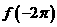 、
、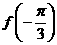 的值;
的值;
(2)
写出函数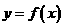 的表达式,作出其图像,并根据图像写出函数的单调区间。
的表达式,作出其图像,并根据图像写出函数的单调区间。
16、(理)从装有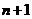 个球(其中
个球(其中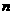 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出 个球
个球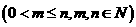 ,共有
,共有 种取法。在这
种取法。在这 种取法中,可以分成两类:一类是取出的
种取法中,可以分成两类:一类是取出的 个球全部为白球,共有
个球全部为白球,共有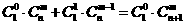 ,即有等式:
,即有等式: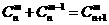 成立。试根据上述思想化简下列式子:
成立。试根据上述思想化简下列式子: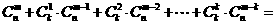 。
。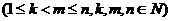 。
。
(文)对于函数的这个性质:1奇函数;2偶函数;3增函数;4减函数,函数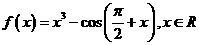 具有的性质的序号是
。(把具有的性质的序号都填上)
具有的性质的序号是
。(把具有的性质的序号都填上)

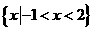 ,N =
,N =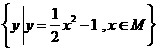 ,
,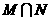 为
(
)
为
(
)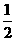 <a<1} C.{a|-1<a<1} D.φ
<a<1} C.{a|-1<a<1} D.φ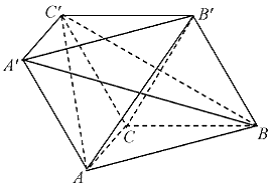 (本小题满分12分)
(本小题满分12分) 中,侧面
中,侧面 底面
底面 ,且
,且 。
。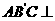 平面
平面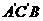 ;
;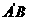 与
与 所成的角。
所成的角。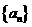 中,
中,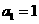 ,前10项和
,前10项和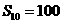 。
。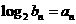 ,问
,问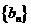 是否未等比数列;并说明理由。
是否未等比数列;并说明理由。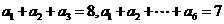 ,记
,记 ,则
,则 。
。 。
。