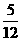18.(本小题满分14分)
已知函数f (x) = (x-a)(x-b)(x-c).
(1) 求证: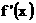 = (x-a)(x-b)+(x-a)(x-c)+(x-b)(x-c);
= (x-a)(x-b)+(x-a)(x-c)+(x-b)(x-c);
(2) 若f (x)是R上的增函数,是否存在点P,使f (x)的图象关于点P中心对称?
如果存在,请求出点P坐标,并给出证明,如果不存在,请说明理由.
17.(本小题满分12分)
小张有一只放有a个红球,b个黄球,c个白球的箱子,且a+b+c =6 (a,b,c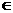 N),小刘有一只放有3个红球,2个黄球,1个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同色时小张胜,异色时小刘胜.
N),小刘有一只放有3个红球,2个黄球,1个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同色时小张胜,异色时小刘胜.
(1) 用a、b、c表示小张胜的概率;
(2) 若又规定当小张取红、黄、白球而胜的得分分别为1分、2分、3分,否则得0分,求小张得分的期望的最大值及此时a、b、c的值.
16.(本小题满分12分)
二次函数f (x)满足f (x+1)-f (x)=2x,且f (0) =1.
(1) 求f (x)的解析式;
(2) 在区间[-1,1]上,y=f (x)的图象恒在y=2x十m的图象上方,试确定实数m的取值范围.
15.购买手机的“全球通”卡,使用时须付“基本月租费”
(每月须交的固定月租费)50元,在市区通话时每分钟另收
话费0.4元;购买“神州行”卡,使用时不收“基本月租费”,
但市区内通话时每分钟另收话费0.6元.若某用户每月手机
费预算为120元,则在这两种手机卡中,购买__________卡
较合算.
14.如图正六边形ABCDEF中,AC∥y轴.从六个顶点中任取三点,使这三点能
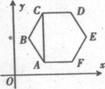 确定一条形如y=ax
2+bx+c (a≠0)的抛物线的概率是_______________.
确定一条形如y=ax
2+bx+c (a≠0)的抛物线的概率是_______________.
11.在平面直角坐标系中,x轴的正半轴上有4个点,y轴的正半轴上有5个点,这9个点任意两点连线,则所有连线段的交点落入第一象限的最多有______个.
10.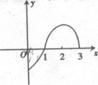 已知函数f (x)是定义在(-3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,则不等式f (x) cosx<0的解集是
已知函数f (x)是定义在(-3,3)上的奇函数,当0<x<3时,f(x)的图象如图所示,则不等式f (x) cosx<0的解集是
A.(-3,-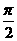 )
) (0,1)
(0,1) (
(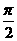 ,3)
,3)
B.(-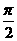 ,一1)
,一1) (0,1)
(0,1) (
(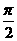 ,3)
,3)
C.(-3,-1) (0,1)
(0,1) (1,3)
(1,3)
D.(-3,-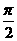 )
) (0,1)
(0,1) (1,3)
(1,3)
第Ⅱ卷 (非选择题 共100分)

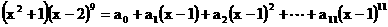 ,则
,则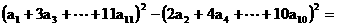 ______(用数字作答).
______(用数字作答).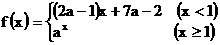 在(-∞,+∞)上单调递减,则实数a的取值范围是_________________.
在(-∞,+∞)上单调递减,则实数a的取值范围是_________________. 的概率是
的概率是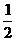 B.
B.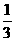 C.
C. 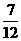 D.
D.