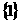6.甲、乙、丙、丁四位同学各自对 、
、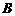 两变量的线性相关性作试验,并用回归分析方法分别求得相关系数
两变量的线性相关性作试验,并用回归分析方法分别求得相关系数 与残差平方和
与残差平方和 如下表:
如下表:
|
|
甲 |
乙 |
丙 |
丁 |
 |
0.82 |
0.78 |
0.69 |
0.85 |
 |
106 |
115 |
124 |
103 |
则哪位同学的试验结果体现 、
、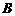 两变量更强的线性相关性?( )
两变量更强的线性相关性?( )

 甲
甲
 乙
乙
 丙
丙  丁
丁
4.有关命题的说法错误的是 ( )
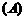 命题“若
命题“若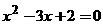 则
则
 ”的逆否命题为:“若
”的逆否命题为:“若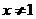 , 则
, 则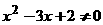 ”.
”.
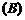 “
“ ”是“
”是“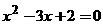 ”的充分不必要条件.
”的充分不必要条件.
 若
若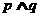 为假命题,则
为假命题,则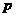 、
、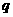 均为假命题.
均为假命题.
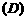 对于命题
对于命题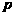 :
: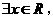 使得
使得 . 则
. 则
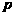 :
: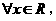 均有
均有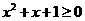 .
.
21.(本小题满分14分)
定义在(-1,1)上的函数f (x)满足:对任意x,y∈(-1,1)都有
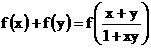
(1) 求证:函数f (x)是奇函数;
(2) 若当x∈(-1,0)时,有f (x)>0,求证:f (x)在(-1,1)上是减函数;
(3) 在(2)的条件下解不等式: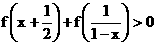 .
.
20.(本小题满分14分)
已知函数y= f (x)对于任意实数x,y都有f (x+y) =f (x)+f (y)+2xy .
(1) 求f (0)的值;
(2) 若f (1)=1,求f (2),f (3),f (4)的值,猜想f(n)的表达式并用数学归纳法证明你的结论(n∈N*);
(3) 若f (1)≥1,求证: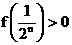 (n∈N*).
(n∈N*).
19.(本小题满分14分)
某公司生产的A型商品通过租赁柜台进入某商场销售.第一年,商场为吸引厂家,决定免收该年管理费,因此,该年A型商品定价为每件70元,年销售量为11.8万件.第二年,商场开始对该商品征收比率为p%的管理费(即销售100元要征收p元),于是该商品的定价上升为每件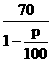 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.
(1) 将第二年商场对该商品征收的管理费y(万元)表示成p的函数,并指出这个函数的定义域;
(2) 要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征收管理费的比率p%的范围是多少?
(3) 第二年,商场在所收管理费不少于14万元的前提下,要让厂家获得最大销售金额,则p应为多少?

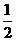

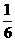
 的值是
( )
的值是
( ) 
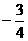
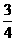
 函数
函数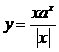
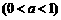 的图象的大致形状是
( )
的图象的大致形状是
( )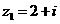 ,
,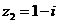 ,则
,则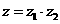 在复平面上对应的点位于( )
在复平面上对应的点位于( )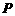 和
和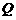 ,表示同一集合的是( )
,表示同一集合的是( )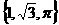 ,
,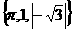
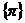 ,
,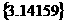
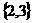 ,
,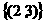
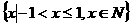 ,
,