19、(本小题满分14分)
已知公比为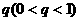 的无穷等比数列
的无穷等比数列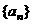 各项的和为9,无穷等比数列
各项的和为9,无穷等比数列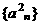 各项的和为
各项的和为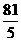 .
.
(Ⅰ)求数列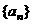 的首项
的首项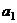 和公比
和公比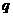 ;
;
(Ⅱ)对给定的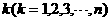 ,设
,设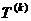 是首项为
是首项为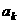 ,公差为
,公差为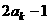 的等差数列.求数列
的等差数列.求数列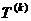 的前10项之和;
的前10项之和;
(Ⅲ)设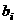 为数列
为数列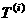 的第
的第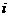 项,
项,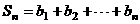 ,求
,求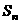 ,并求正整数
,并求正整数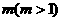 ,使得
,使得
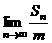 存在且不等于零.
存在且不等于零.
(注:无穷等比数列各项的和即当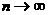 时该无穷数列前n项和的极限)
时该无穷数列前n项和的极限)
19解: (Ⅰ)依题意可知,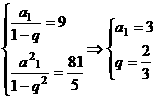
(Ⅱ)由(Ⅰ)知,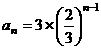 ,所以数列
,所以数列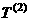 的的首项为
的的首项为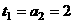 ,公差
,公差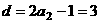 ,
,
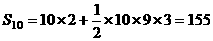 ,即数列
,即数列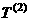 的前10项之和为155.
的前10项之和为155.
(Ⅲ) 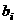 =
=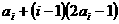 =
=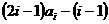 =
=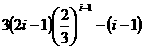 ,
,
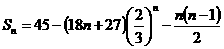 ,
,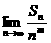 =
=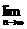
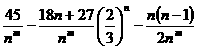
当m=2时,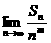 =-
=-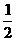 ,当m>2时,
,当m>2时,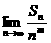 =0,所以m=2
=0,所以m=2
- 答案

