22.  (本大题满分14分)
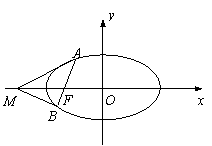
如图,过椭圆
(本大题满分14分)
如图,过椭圆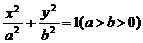 的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
(1)求椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB,若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
(1)求椭圆 的“左特征点”M的坐标;
(2)试根据(1)中的结论猜测:椭圆
的“左特征点”M的坐标;
(2)试根据(1)中的结论猜测:椭圆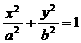
 的“左特征点”M是一个怎样的点?并证明你的结论.
的“左特征点”M是一个怎样的点?并证明你的结论.
21. (本大题满分12分)
已知 是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)求c的值;
(2)在函数f (x)的图象上是否存在一点M(x0,y0),使得f (x)在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由;
(3)求|
AC |的取值范围.
是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为 (2,0),且f (x) 在[-1,0]和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)求c的值;
(2)在函数f (x)的图象上是否存在一点M(x0,y0),使得f (x)在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由;
(3)求|
AC |的取值范围.
20. (本大题满分12分)
已知数列{an}的各项均为正数且a1 = 6,点 在抛物线
在抛物线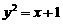 上;数列{bn}中,点
上;数列{bn}中,点 在过点(0,1)且方向向量为(1,2)的直线上.
(1)求数列{an}、{bn}的通项公式;
(2)对任意正整数n,不等式
在过点(0,1)且方向向量为(1,2)的直线上.
(1)求数列{an}、{bn}的通项公式;
(2)对任意正整数n,不等式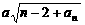 ≤
≤ …
…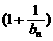 成立,求正数a的取值范围.
成立,求正数a的取值范围.
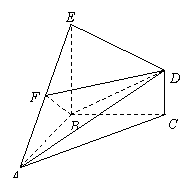
19. (本大题满分12分) 如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC = 90°,BE和CD都垂直于平面ABC,且BE = AB = 2,CD = 1,点F是AE的中点. (1)求证:DF∥平面ABC; (2)求AB与平面BDF所成角的大小.
18. (本大题满分12分)
设一汽车在行进途中要经过4个路口,汽车在每个路口遇到绿灯的概率为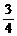 ,遇到红灯(禁止通行)的概率为
,遇到红灯(禁止通行)的概率为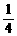 .假定汽车只在遇到红灯或到达目的地才停止前进,
.假定汽车只在遇到红灯或到达目的地才停止前进,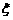 表示停车时已经通过的路口数,求:
(1)
表示停车时已经通过的路口数,求:
(1)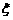 的概率的分布列及期望E
的概率的分布列及期望E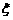 ;
(2)停车时最多已通过3个路口的概率.
;
(2)停车时最多已通过3个路口的概率.
16. 霓虹灯的一个部位由七个小灯泡组成(如右图),每个灯泡均可亮出红色或黄色.现设计每次变换只闪亮其中三个灯泡,且相邻两个不同时亮,则一共可呈现 种不同的变换形式(用数字作答).
15.
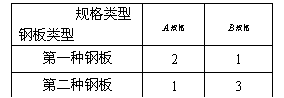 将大小不同的两种钢板截成A、B两种规格的成品,每张钢板可同时截得这两种规格的成品的块数如右表所示.现在需要A、B两种规格的成品分别为12块和10块,则至少需要这两种钢板共 张.
将大小不同的两种钢板截成A、B两种规格的成品,每张钢板可同时截得这两种规格的成品的块数如右表所示.现在需要A、B两种规格的成品分别为12块和10块,则至少需要这两种钢板共 张.
|
○○○○○○○ |

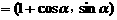 ,b
,b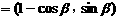 ,c = (1,0),其中
,c = (1,0),其中 ,
,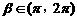 .若a与c的夹角为
.若a与c的夹角为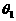 ,b与c的夹角为
,b与c的夹角为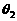 ,且
,且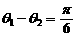 ,求
,求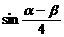 的值.
的值.
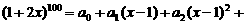 …
…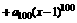 ,则
,则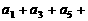 …
…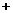
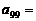 .
.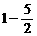 k)e2和b = 2e1 + 3e2是两个共线向量,则实数k = .
k)e2和b = 2e1 + 3e2是两个共线向量,则实数k = .