18. (本大题满分12分)
已知数列{an}的前n项和为Sn,且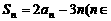 N*).
(1)证明:数列{an+3}是等比数列;
(2)数列{an}中是否存在三项成等差数列?若存在,请求出一组;若不存在,请说明理由.
N*).
(1)证明:数列{an+3}是等比数列;
(2)数列{an}中是否存在三项成等差数列?若存在,请求出一组;若不存在,请说明理由.
17. (本大题满分12分)
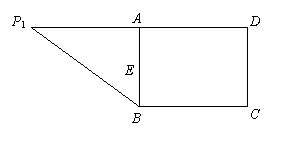
已知向量m=(sin B,1-cos B),且与向量n=(1,0)所成角为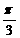 ,其中A、B、C是
,其中A、B、C是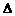 ABC的内角,求
ABC的内角,求 的取值范围.
的取值范围.
16.
已知a、b为不垂直的异面直线,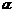 是一个平面,则a、b在
是一个平面,则a、b在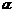 上的射影有可能是:
①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点.
在上面结论中,正确结论的编号是 * (写出所有正确结论的编号).
上的射影有可能是:
①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点.
在上面结论中,正确结论的编号是 * (写出所有正确结论的编号).
13. 某中学有高一学生400人,高二学生300人,高三学生300人,现通过分层抽样抽取一样本容量为n的样本,已知每个学生被抽到的概率为0.2,则n= * .
12. 若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y=x2,值域为{1,4}的“同族函数”共有 A.9个 B.8个 C.5个 D.4个
第 Ⅱ 卷(非选择题,共90分)
第Ⅱ卷共2页,用黑色签字笔直接答在答题卷每题对应的答题区域内;如需改动,先划掉原来的答案,然后写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.
11. 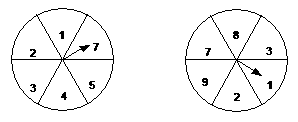 如图所示,在两个圆盘中同时转动指针,当指针停止时落在本圆盘每个数所在区域的机会均等,那么当指针停止时,两个指针同时落在奇数所在区域的概率是
A.
如图所示,在两个圆盘中同时转动指针,当指针停止时落在本圆盘每个数所在区域的机会均等,那么当指针停止时,两个指针同时落在奇数所在区域的概率是
A.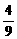 B.
B.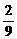 C.
C.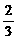 D.
D.
10. 若不等式|x-1|<a成立的充分条件为0<x<4,则实数a的取值范围为 A.[3,+∞) B.[1,+∞) C.(-∞,3] D.(-∞,1]
9. 如图,南北方向的公路l,A地在公路的正东2km处,B地在A地东偏北30°方向2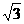 km处, 河流沿岸PQ上任一点到公路l和到A地距离相等.现要在曲线PQ上选一处M建一座码头,向A、B两地转运货物,经测算从M到A、M到B修建公路的费用均为a万元/km,那么修建这两条公路的总费用最低是
A.
km处, 河流沿岸PQ上任一点到公路l和到A地距离相等.现要在曲线PQ上选一处M建一座码头,向A、B两地转运货物,经测算从M到A、M到B修建公路的费用均为a万元/km,那么修建这两条公路的总费用最低是
A.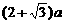 万元 B.
万元 B.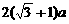 万元
C.5a万元 D.6a万元
万元
C.5a万元 D.6a万元

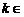 * 时,
* 时,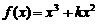 在[0,2]上是减函数.
在[0,2]上是减函数.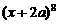 的展开式中,
的展开式中,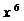 项的系数是448,则正实数a的值为 * .
项的系数是448,则正实数a的值为 * .