3. 一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜,记三种盖法屋顶面积分别为P1、P2、P3.
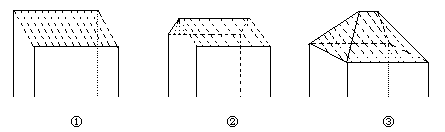
若屋顶斜面与水平面所成的角都是α,则
[ ]
A.P3>P2>P1 B.P3>P2=P1
C.P3=P2>P1 D.P3=P2=P1
2. 已知函数f(x)定义域为R,则下列命题:
①y=f(x)为偶函数,则y=f(x+2)的图象关于y轴对称.
②y=f(x+2)为偶函数,则y=f(x)关于直线x=2对称.
③若函数f(2x+1)是偶函数,则f(2x)的图象关于直线  对称.
④若f(x-2)=f(2-x),则y=f(x)关于直线x=2对称.
⑤y=f(x-2)和y=f(2-x)的图象关于x=2对称.
其中正确的命题序号是( )
A、①②④ B、①③④ C、②③⑤ D、②③④
对称.
④若f(x-2)=f(2-x),则y=f(x)关于直线x=2对称.
⑤y=f(x-2)和y=f(2-x)的图象关于x=2对称.
其中正确的命题序号是( )
A、①②④ B、①③④ C、②③⑤ D、②③④
1. 已知数列 ,那么“对任意的
,那么“对任意的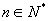 ,点
,点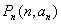 都在直线
都在直线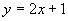 上”是“
上”是“ 为等差数列”的 ( )
(A)必要而不充分条件 (B)充分而不必要条件
(C)充要条件 (D)既不充分也不必要条件
为等差数列”的 ( )
(A)必要而不充分条件 (B)充分而不必要条件
(C)充要条件 (D)既不充分也不必要条件
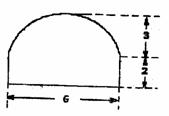
22.如图,一条隧道横截面由一段抛物线及矩形的三边围成,各段长度见图中所示(单位:米)某卡车空载时能通过此隧道.
(1)现有一集装箱,箱宽3米,装上卡车后,箱顶高4.5米,问此车能否通过这条隧道?
(2)若卡车载货板离地面1.4米,为安全起见,集装箱顶与隧道顶部距离不少于0.1米,在可以通过隧道的情况下,长、宽各为多少米的集装箱截面积最大?
20.已知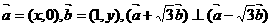 ,
,
(1)求点P(x,y)的轨迹C的方程;
(2)若直线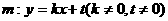 与曲线C交于A、B两点,已知点D(0,-1)
与曲线C交于A、B两点,已知点D(0,-1)
且有|AD|=|BD|,试求t的取值范围.
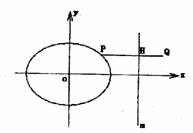 21.如图,过椭圆:
21.如图,过椭圆: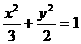 上任一点P,作E的右准线m的垂线PH(H为垂足),
上任一点P,作E的右准线m的垂线PH(H为垂足),
延长PH到Q,使HQ=λPH(λ>0).
(1)求当P在E上运动时,点Q的轨迹G的方程.
(2)若轨迹G是与椭圆E离心率相等的椭圆,求λ的值.
18.在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=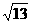 ,SB=
,SB=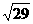
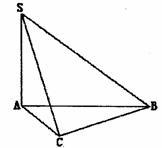 (1)证明:SC⊥BC;
(1)证明:SC⊥BC;
(2)求侧面SBC与底面ABC所成二面角大小;
(3)求异面直线SC与AB所成角的大小.
(用反三角函数表示)
16.过抛物线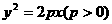 焦点F的直线与抛物线交于P、Q,由P、Q分别引其准线的垂线PH1、QH2垂足分别为H1、H2,H1H2的中点为M,记|PF|=a,|QF|=b,则|MF|=
焦点F的直线与抛物线交于P、Q,由P、Q分别引其准线的垂线PH1、QH2垂足分别为H1、H2,H1H2的中点为M,记|PF|=a,|QF|=b,则|MF|=
。

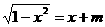 没有实数解,则实数m的取值范围是
没有实数解,则实数m的取值范围是  (B)
(B) 
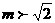 (D)
(D)
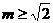
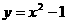 上的定点,P、Q为动点,且在抛物线上,
上的定点,P、Q为动点,且在抛物线上, .
.