8. 设△ABC的一个顶点是A(3,-1),∠B,∠C的平分线方程分别是x=0,y=x,则直线BC的方程是 ( )
A.y=2x+5 B.y=2x+3 C.y=3x+5 D.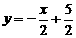
5.
已知a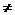 b,且a
b,且a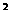 sin
sin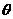 +acos
+acos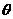 -
-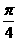 =0 ,b
=0 ,b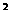 sin
sin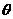 +bcos
+bcos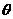 -
-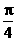 =0,则连接(a,a
=0,则连接(a,a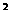 ),
),
(b,b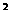 )两点的直线与单位圆的位置关系是
( )
)两点的直线与单位圆的位置关系是
( )
A.相交 B.相切 C.相离 D.不能确定
4.
定义在R上的函数y=f(x),在(-∞,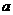 )上是增函数,且函数 y=f(x+
)上是增函数,且函数 y=f(x+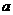 )是偶函数,当x1<
)是偶函数,当x1<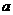 ,x2>
,x2>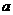 且
且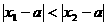 时,有
( )
时,有
( )
A.f(2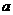 -x1)> f(2
-x1)> f(2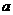 -x2) B.f(2
-x2) B.f(2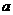 -x1)= f(2
-x1)= f(2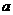 -x2)
-x2)
C.f(2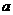 -x1)< f(2
-x1)< f(2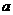 -x2) D.-f(2
-x2) D.-f(2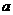 -x1)< f(x2-2
-x1)< f(x2-2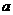 )
)
3. 对“a、b、c是不全相等的正数”,给出下列判断:
①(a-b)2+(b-c)2+(c-a)2≠0; ②a>b与a<b及a≠c中至少有一个成立;
③a≠c,b≠c,a≠b不能同时成立.
其中判断正确的个数为 ( )
A.0个 B.1个 C.2个 D.3个
1.
已知实数a、b、c满足b+c=6-4a+3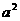 ,c-b=4-4a+
,c-b=4-4a+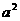 ,则a、b、c的大小关系是
( )
,则a、b、c的大小关系是
( )
A.c≥b>a B.a>c≥b C.c>b>a D.a>c>b
22. (文)如图甲、乙连接的6个元件,它们断电的概率第一个为P1=0.6,第二个为P2=0.2,其余四个都为P=0.3.分别求甲断电、乙通电的概率.

(理)已知a>1,数列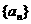 的通项公式是
的通项公式是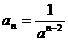 ,前n项和记作
,前n项和记作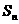 (n=1,2,…),规定
(n=1,2,…),规定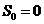 .函数
.函数 在
在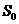 处和每个区间(
处和每个区间(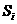 ,
,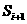 )(i=0,1,2,…)上有定义,且
)(i=0,1,2,…)上有定义,且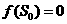 ,
,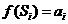 (i=1,2,…).当
(i=1,2,…).当 (
(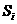 ,
,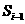 )时,f(x)的图像完全落在连结点
)时,f(x)的图像完全落在连结点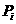 (
(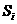 ,
,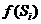 )与点
)与点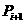 (
(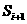 ,
,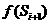 )的线段上.
)的线段上.
(Ⅰ)求f(x)的定义域;
(Ⅱ)设f(x)的图像与坐标轴及直线l: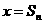 (n=1,2,…)围成的图形面积为
(n=1,2,…)围成的图形面积为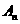 ,
,
求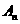 及
及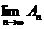 ;
;
(Ⅲ)若存在正整数n,使得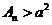 ,求a的取值范围.
,求a的取值范围.

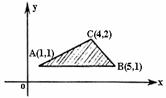 在如图所示的坐标平面的可行域(阴影部分且包括边界)内,目标函数
在如图所示的坐标平面的可行域(阴影部分且包括边界)内,目标函数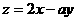 取得最大值的最优解有无数个,则a为
( )
取得最大值的最优解有无数个,则a为
( )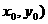 为圆
为圆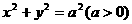 内异于圆心的一点,则直线
内异于圆心的一点,则直线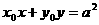 与该圆的位置关系为 ( )
与该圆的位置关系为 ( )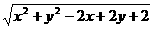 的最小值为 ( )
的最小值为 ( )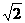 B.4 C.2
B.4 C.2