1.
天文台用3.2万元买一台观测仪,已知这台观测仪从启用的第一天起连续使用,第n天的维修保养费为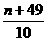 元(n∈N*),使用它直至报废最合算(所谓报废最合算是指使用的这台仪器的平均耗资最少)为止,一共使用了
( )
元(n∈N*),使用它直至报废最合算(所谓报废最合算是指使用的这台仪器的平均耗资最少)为止,一共使用了
( )
A.800天 B.1000天 C.1200天 D.1400天
22. 已知点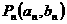 都在直线
都在直线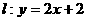 上,
上,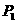 为直线
为直线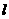 与
与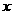 轴的交点,数列
轴的交点,数列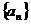 成等差数列,公差为1. (
成等差数列,公差为1. (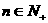 )
)
(1)求数列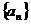 ,
,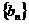 的通项公式;
的通项公式;
(2)若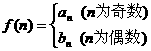 , 问是否存在
, 问是否存在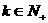 ,使得
,使得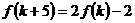 成立;若存在,求出
成立;若存在,求出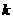 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(3)求证: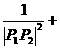
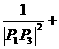 …… +
…… +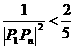 (
(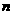
 2,
2, 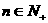 )
)
21. 设关于x的一元二次方程2x2-ax-2=0的两根的α、β(α<β),函数f(x)=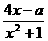
⑴求f(α)·f(β)的值;
⑵证明f(x)是[α,β]的增函数;
(3)当a为何值时,f(x)在区间[α,β]上的最大值与最小值之差最小?
19. 已知函数: .
.
(1)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立;
(2)当f(x)的定义域为[a+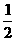 ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];
(3)设函数g(x)=x2+|(x-a)f(x)| ,求g(x) 的最小值 .
18.甲、乙两人进行五次比赛,如果甲或乙无论谁胜了三次,比赛宣告结束。假定甲获胜的概率是 ,乙获胜的概率是
,乙获胜的概率是 ,试求下列概率。
,试求下列概率。
(I)比赛以甲3胜1败而结束的概率;
(II)比赛以乙3胜2败而结束的概率;
(III)设甲先胜3次的概率为a,乙先胜3次的概率为b,求a:b的值。
16. 设坐标平面内有一个质点从原点出发,沿x轴跳动,每次向正方向或负方向跳1个单位,经过5次跳动质点落在点(3,0)(允许重复过此点)处,则质点不同的运动方法共有________种(用数字作答)。

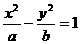 的离心率e等于
( )
的离心率e等于
( )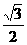 B.
B.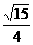 C.
C.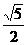 D.
D.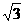
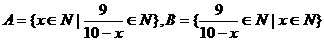 ,试问集合A与B共有几个相同的元素,并写出由这些“相同元素”组成的集合.
,试问集合A与B共有几个相同的元素,并写出由这些“相同元素”组成的集合.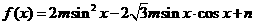 的定义域为
的定义域为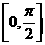 ,值域为
,值域为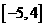 .试求函数
.试求函数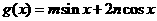 (
(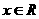 )的最小正周期和最值
)的最小正周期和最值