21、设函数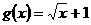 ,函数
,函数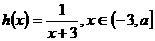 ,其中
,其中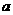 为常数且
为常数且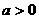 ,令函数
,令函数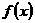 为函数
为函数 和
和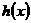 的积函数。
的积函数。
(1)求函数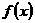 的表达式,并求其定义域;
的表达式,并求其定义域;
(2)当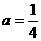 时,求函数
时,求函数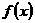 的值域;
的值域;
(3)是否存在自然数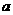 ,使得函数
,使得函数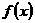 的值域恰为
的值域恰为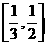 ?若存在,试写出所有满足条件的自然数
?若存在,试写出所有满足条件的自然数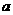 所构成的集合;若不存在,试说明理由。
所构成的集合;若不存在,试说明理由。
解:(1)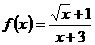 ,
,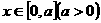 。
。
(2)∵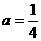 ,∴函数
,∴函数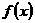 的定义域为
的定义域为 ,令
,令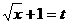 ,则
,则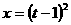 ,
,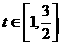 ,
,
∴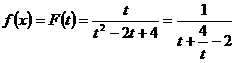 ,
,
∵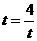 时,
时,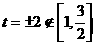 ,又
,又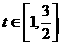 时,
时,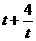 递减,∴
递减,∴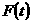 单调递增,
单调递增,
∴ ,即函数
,即函数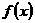 的值域为
的值域为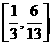 。
。
(3)假设存在这样的自然数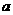 满足条件,令
满足条件,令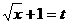 ,则
,则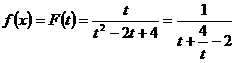 ,
,
∵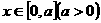 ,则
,则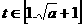 ,要满足值域为
,要满足值域为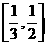 ,则要满足
,则要满足 ,
,
由于当且仅当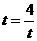
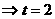 时,有
时,有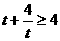 中的等号成立,且此时
中的等号成立,且此时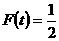 恰为最大值,
恰为最大值,
∴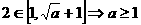 ,
,
又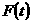 在
在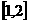 上是增函数,在
上是增函数,在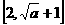 上是减函数,∴
上是减函数,∴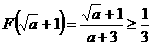
 ,
,
综上,得 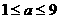 。
。
20、人口问题其实是许多国家的政府都要面对的问题。05年10月24日出版的《环球时报》就报道了一篇俄罗斯政府目前遭遇“人口危机”的文章。报道中引用了以下来自俄政府公布的数据:
●截至05年6月底,俄罗斯人口为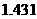 亿,人口密度每平方公里只有
亿,人口密度每平方公里只有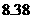 人;
人;
●04年一年俄人口就减少了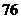 万,05年1月至5月共又减少了
万,05年1月至5月共又减少了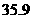 万;
万;
●据俄联邦安全会议预测,到2050年,俄将只有约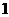 亿人口,比目前锐减
亿人口,比目前锐减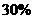 。
。
试根据以上数据信息回答下列问题:
(1)以04年至05年5月这17个月平均每月人口减少的数据为基础,假设每月人口减少相同,预测到2050年6月底,俄罗斯的人口约为多少亿?(保留三位小数)
(2)按第(1)小题给定的预测方法,到何时俄罗斯的人口密度将低于每平方公里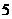 人?
人?
解:(1)由给出的信息可知,17个月里平均每月人口减少 万人,
万人,
2005年6月底至2050年6月底共经过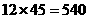 个月,若每月人口减少数相同,
个月,若每月人口减少数相同,
则到2050年6月底俄罗斯的人口数约为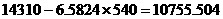 万,即约为
万,即约为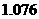 亿。
亿。
(2)设从05年6月底起,经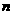 个月后俄罗斯的人口密度将低于每平方公里
个月后俄罗斯的人口密度将低于每平方公里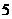 人,
人,
于是有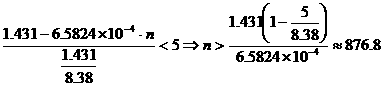 ,
,
∴至少要经过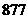 个月,即
个月,即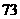 年零
年零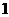 个月,也就是到2078年7月底,俄罗斯的人口密度将低于每平方公里
个月,也就是到2078年7月底,俄罗斯的人口密度将低于每平方公里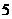 人。
人。
18、在平面直角坐标系 中,已知抛物线
中,已知抛物线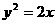 的焦点为
的焦点为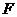 ,抛物线上一点
,抛物线上一点 的横坐标为
的横坐标为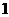 ,直线
,直线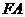 与抛物线交于点
与抛物线交于点 、
、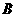 ,求向量
,求向量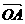 和
和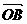 夹角的大小。
夹角的大小。
解: ,由抛物线的对称性,不妨设
,由抛物线的对称性,不妨设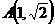 ,则直线
,则直线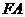 的方程为
的方程为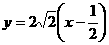 ,
,
把它代入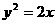 ,得
,得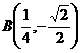 ,则
,则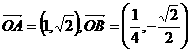 ,设向量
,设向量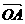 和
和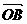 夹角为
夹角为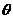 ,
,
则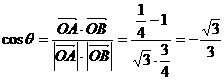 ,由对称性,当
,由对称性,当 时,结论相同。
时,结论相同。
∴向量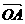 和
和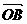 夹角的大小为
夹角的大小为 。
。
12、如图,已知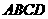 和
和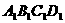 都是正方形,且
都是正方形,且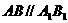 ,
,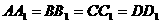 ,
,
若将图中已作出的线段的两个端点分别作为向量的始点和终点所形成的不相等的向量的全体
构成集合M,则从集合M中任取两个向量恰为平行向量的概率是 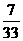 (用分数表示结果)。
(用分数表示结果)。

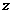 同时满足:①
同时满足:①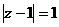 ;②
;②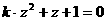 (
(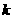 为实数且
为实数且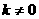 )。
)。 同时满足两个条件,
同时满足两个条件, 与假设
与假设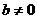 矛盾,
矛盾, ,求:
,求: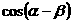 。
。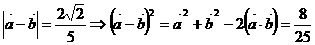 ,又由条件得
,又由条件得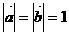 ,∴
,∴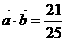 ,
,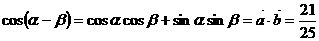 。
。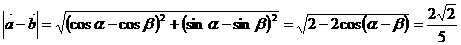 ,
, 。
。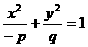 表示双曲线,则下列方程所表示的椭圆中,与此双曲线有共同焦点的是 (
C )
表示双曲线,则下列方程所表示的椭圆中,与此双曲线有共同焦点的是 (
C )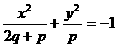 ; B,
; B,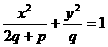 ; C,
; C,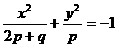 ; D,
; D,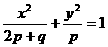 。
。 上的函数
上的函数 ,且当
,且当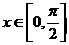 时,
时,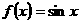 ,则
,则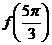 的值为
( D
)
的值为
( D
)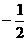 ;
B,
;
B,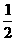 ;
C,
;
C,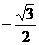 ;
D,
;
D,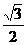 。
。 中,
中,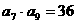 ,且
,且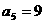 ,则
,则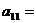 (
B )
(
B )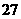 ;
B,
;
B,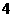 ;
C,
;
C,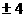 ;
D,
;
D,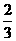 。
。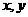 都是实数,则“
都是实数,则“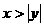 ”是“
”是“ ”的 条件
( A
)
”的 条件
( A
)