科目:,来源:,题型:
22、已知二次函数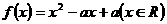 同时满足:①不等式
同时满足:①不等式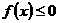 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在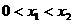 ,使得不等式
,使得不等式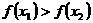 成立。
成立。
设数列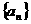 的前
的前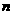 项和
项和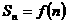 ,
,
(1)求数列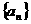 的通项公式;
的通项公式;
(2)试构造一个数列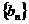 ,(写出
,(写出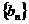 的一个通项公式)满足:对任意的正整数
的一个通项公式)满足:对任意的正整数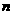 都有
都有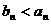 ,且
,且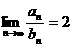 ,并说明理由;
,并说明理由;
(3)设各项均不为零的数列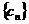 中,所有满足
中,所有满足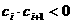 的正整数
的正整数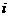 的个数称为这个数列
的个数称为这个数列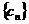 的变号数。令
的变号数。令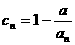 (
(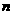 为正整数),求数列
为正整数),求数列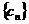 的变号数。
的变号数。
解:(1)∵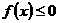 的解集有且只有一个元素,∴
的解集有且只有一个元素,∴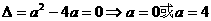 ,
,
当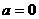 时,函数
时,函数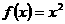 在
在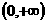 上递增,故不存在
上递增,故不存在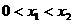 ,使得不等式
,使得不等式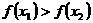 成立。
成立。
当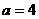 时,函数
时,函数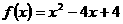 在
在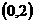 上递减,故存在
上递减,故存在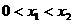 ,使得不等式
,使得不等式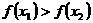 成立。
成立。
 综上,得
综上,得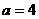 ,
,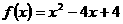 ,∴
,∴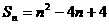 ,∴
,∴
(2)要使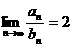 ,可构造数列
,可构造数列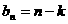 ,∵对任意的正整数
,∵对任意的正整数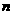 都有
都有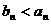 ,
,
∴当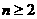 时,
时,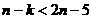 恒成立,即
恒成立,即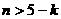 恒成立,即
恒成立,即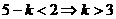 ,
,
又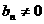 ,∴
,∴ ,∴
,∴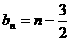 ,等等。
,等等。
(3)解法一:由题设 ,
,
∵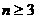 时,
时,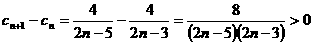 ,∴
,∴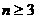 时,数列
时,数列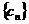 递增,
递增,
∵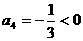 ,由
,由 ,可知
,可知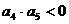 ,即
,即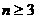 时,有且只有
时,有且只有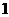 个变号数;
个变号数;
又∵ ,即
,即 ,∴此处变号数有
,∴此处变号数有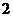 个。
个。
综上得 数列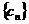 共有
共有 个变号数,即变号数为
个变号数,即变号数为 。
。
解法二:由题设 ,
,
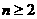 时,令
时,令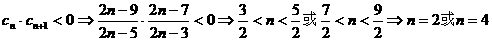 ;
;
又∵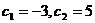 ,∴
,∴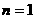 时也有
时也有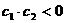 。
。
综上得 数列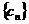 共有
共有 个变号数,即变号数为
个变号数,即变号数为 。
。
点击展开完整题目
试题详情

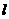 过点
过点 ,当直线
,当直线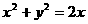 有两个公共点时,其斜率
有两个公共点时,其斜率 的取值范围是
的取值范围是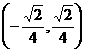 。
。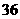 种。
种。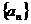 的前
的前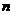 项和
项和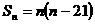 ,则
,则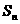 的最小值为
的最小值为 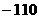 (结果用数值表示)。
(结果用数值表示)。 的解是
的解是 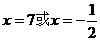 。
。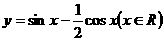 的最大值为
的最大值为 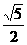 。
。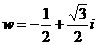 ,则
,则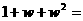
 。
。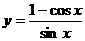 的最小正周期是
的最小正周期是 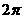 。
。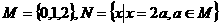 ,则集合
,则集合
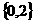 。
。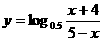 的定义域为
的定义域为 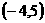 。
。