科目:,来源:,题型:
22、已知函数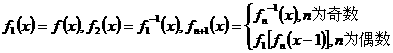 ,
,
(1)若函数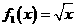 ,求函数
,求函数 的解析式;
的解析式;
(2)(理)若函数 ,函数
,函数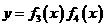 的定义域是
的定义域是 ,求
,求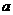 的值;
的值;
(文)若函数 ,求函数
,求函数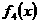 的定义域;
的定义域;
(3)设 是定义在
是定义在 上的周期为4的奇函数,且函数
上的周期为4的奇函数,且函数 的图像关于直线
的图像关于直线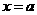 对称,
对称,
当 ,求正数
,求正数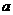 的最小值及函数
的最小值及函数 在
在 上的解析式。
上的解析式。
解:(1)∵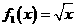 ,
, ,∴
,∴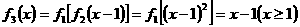 ,
,
 ,
,
(2) (理)

 ,
,
∴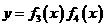 的定义域是
的定义域是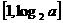 ,∴
,∴ ,即
,即 。
。
(文)

 ,函数
,函数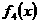 的定义域是
的定义域是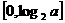 。
。
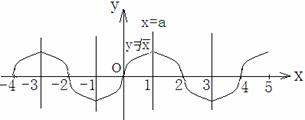 (3) 据题意,作图如下:
(3) 据题意,作图如下:
 可知正数
可知正数
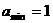 。
。
函数 在
在 上的解析式了
。
上的解析式了
。
点击展开完整题目
试题详情
科目:,来源:,题型:
21、已知在数列 中,
中, (
(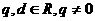 )
)
(1)若 ,求
,求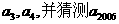 ;
;
(2)(理)若 是等比数列,且
是等比数列,且 是等差数列,求
是等差数列,求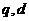 满足的条件;
满足的条件;
(文) ,若
,若 是等比数列,且
是等比数列,且 是等差数列,求
是等差数列,求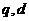 满足的关系式;
满足的关系式;
(3)一个质点从原点出发,依次按向右、向上、向左、向下的方向交替地运动,第 次运动的位移是
次运动的位移是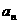 ,质点到达点
,质点到达点 ,设点
,设点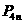 的横坐标为
的横坐标为 ,若
,若 ,求
,求 。
。
解:(1)∵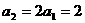 ,∴
,∴ ,
, ,猜测
,猜测 。
。
(2)(理) ,当
,当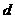 =0,显然成立;当
=0,显然成立;当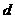
 0,
0, ,则
,则 ;
;
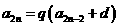 ,当
,当 ,显然成立;当
,显然成立;当 ,
, 。
。
(文)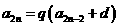 ,
, ,
, 。
。
(3) ,则
,则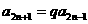 ,∵
,∵ ,∴
,∴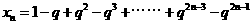 ,
,
由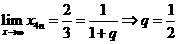 。
。
点击展开完整题目
试题详情
科目:,来源:,题型:
20、现有一批货物用轮船从上海洋山深水港运往青岛,已知该船航行的最大速度为35海里/小时,上海至青岛的航行距离约为500海里,每小时运输成本由燃料费用和其余费用组成。轮船每小时使用的燃料费用与轮船速度的平方成正比(比例系数为0.6),其余费用每小时960元。
(1)把全程运输成本y(元)表示为速度 (海里/小时)的函数;
(海里/小时)的函数;
(2)为了使全程运输成本最小,轮船应以多大速度行驶。
解:(1)
 (
( )
)
(2)先证明其在 上为减函数,则
上为减函数,则 时,取得最小值。答:略。
时,取得最小值。答:略。
点击展开完整题目
试题详情

 的最小正周期是
的最小正周期是  。
。
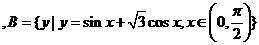 ,求
,求
 ,
, )
) ,B=
,B=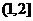 ,∴
,∴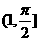 。
。 有一实根为
有一实根为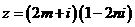 ,
,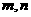 的值及复数
的值及复数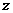 的模。
的模。 ,∴
,∴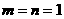 ,
,  ,∴
,∴ 。
。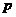 :函数
:函数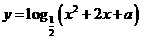 的值域为
的值域为 是减函数,若
是减函数,若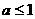 B.
B.
 C.
C.
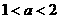 D.
D.
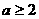
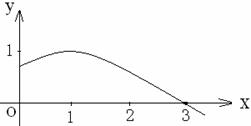 函数
函数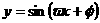 的部分图象如图,则
的部分图象如图,则 、
、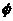 可以取的
可以取的 B、
B、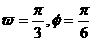
 D、
D、
 ,则
,则 在复平面内的对应点位于
( D )
在复平面内的对应点位于
( D )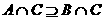 ”是“
”是“ ”的
(
”的
(  )
)