3.设M={平面内的点(a,b)},N={f(x)|f(x)=acos2x+bsin2x} ,给出M到N的映射:
f:(a,b)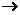 f(x)= acos2x+bsin2x。则点(1,)的象f(x)的最小正周期为:
f(x)= acos2x+bsin2x。则点(1,)的象f(x)的最小正周期为:
A.π B.2π C. D.
22.(本小题满分14分)
已知等比数列{a n}的首项为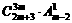 ,公比是
,公比是 展开式中第二项.
展开式中第二项.
(1)用n和x表示数列{a n}的通项a n;
(2)若数列{an}的前n项和为Sn,用n和x表示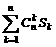 ;
;
(3)若g(x)=(x-1)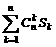 ,其导数为g/(x),且0<x<1,求证:
,其导数为g/(x),且0<x<1,求证: <2n[
<2n[ .
.
21.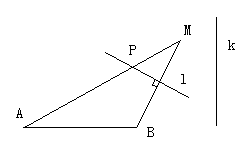
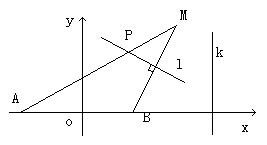 (本小题满分12分) 已知如图, A,B为两个定当,且
(本小题满分12分) 已知如图, A,B为两个定当,且 =2,动点M到A点的距离是4,线段MB的垂直平分线
=2,动点M到A点的距离是4,线段MB的垂直平分线 交MA与点P,直线k
交MA与点P,直线k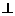 AB,且点B到直线k的距离为3。
AB,且点B到直线k的距离为3。
(1) 求证:点P到点B的距离与到直线K的距离的比为定值。
(2) 若点P到A,B两点的距离之积为m,当m取最大值时,求P点的坐标
(3)
若
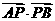 .
.
20、(本小题满分12分)已知函数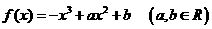
(Ⅰ)是否存在实数使函数 在R上是单调函数?
在R上是单调函数?
(Ⅱ)若x∈[0,1],函数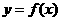 上任意一点切线的斜率为k,讨论|k|≤1的充要条件.
上任意一点切线的斜率为k,讨论|k|≤1的充要条件.
19、(本小题满分12分)正四面体A-BCD的棱长为1,
(Ⅰ)如图(1)M为CD中点,求异面直线AM与BC所成的角;
(Ⅱ)将正四面体沿AB、BD、DC、BC剪开,作为正四棱锥的侧面如图(2),求二面角M-AB-E的大小;
(Ⅲ)若将图(1)与图(2)面ACD重合,问该几何体是几面体
(不需要证明),并求这几何体的体积。


17.甲乙两名篮球运动员,投篮命中率分别是0.9与0.8。
(1)如果每人投篮一次,求甲、乙两人至少有一人进球的概率。
(2)如果每人投篮3次,求甲投进2球且乙投进一球的概率。(结果保留两个有效数字)

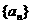 的前n项和记为
的前n项和记为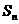 ,若
,若 为一个确定的常数,则下列各数中也是常数的是
为一个确定的常数,则下列各数中也是常数的是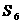 B.
B. 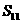 C.
C. 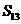 D.
D.
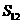
 以下四图,都是同一坐标系中三次函数及其导函数的图象,其中一定不正确的序号是
以下四图,都是同一坐标系中三次函数及其导函数的图象,其中一定不正确的序号是 。
。