17.解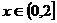 时,
时,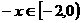 , 则
, 则 
∵函数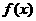 是定义在
是定义在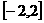 上的奇函数,即
上的奇函数,即
∴ ,即
,即 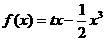 ,又可知
,又可知 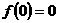
∴函数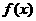 的解析式为
的解析式为 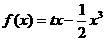 ,
,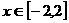
(2)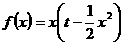 ,∵
,∵ ,
,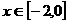 ,∴
,∴
∵ 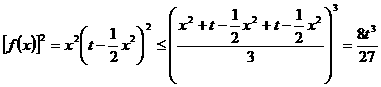
∴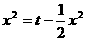 ,即
,即 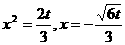
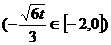 时,
时,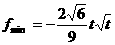 。
。
猜想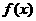 在
在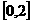 上的单调递增区间为
上的单调递增区间为 。
。
(3) 时,任取
时,任取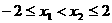 ,∵
,∵
∴ 在
在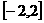 上单调递增,即
上单调递增,即 ,即
,即
∵ ,∴
,∴ ,∴
,∴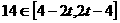
∴当 时,函数
时,函数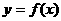 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线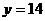 上
上
.18. (1)解:以O为原点,OA为x轴建立直角坐标系,设A(2,0),
则椭圆方程为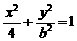 --------------------------- 2分
--------------------------- 2分
∵O为椭圆中心, ∴由对称性知|OC|=|OB|
又∵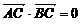 , ∴AC⊥BC
, ∴AC⊥BC
又∵|BC|=2|AC|, ∴|OC|=|AC|
∴△AOC为等腰直角三角形
∴点C的坐标为(1,1) ∴点B的坐标为(-1,-1) --------------------------------- 4分
将C的坐标(1,1)代入椭圆方程得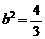 ,
,
则求得椭圆方程为 ------------------------------------------------------------- 6分
------------------------------------------------------------- 6分
(2)证:由于∠PCQ的平分线垂直于OA(即垂直于x轴),
不妨设直线PC的斜率为k,则直线QC的斜率为-k,
因此直线PC、QC的方程分别为y=k(x-1)+1,y=-k(x-1)+1
由 得:
得:
(1+3k2)x2-6k(k-1)x+3k2-6k-1=0 (*)--------------------------------------------8分
∵点C(1,1)在椭圆上, ∴x=1是方程(*)的一个根,
∴xP•1=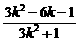 即
xP=
即
xP=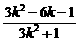
同理xQ=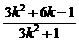 -------------------------------------------------------------------- 10分
-------------------------------------------------------------------- 10分
∴直线PQ的斜率为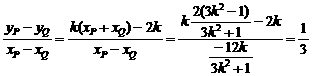 ---------12分
---------12分
又∵ ,∴
,∴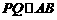 .---------------------------------------------------13分
.---------------------------------------------------13分
18.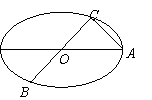 如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且
如图所示,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且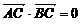 ,|BC|=2|AC|.
(1)建立适当的坐标系,求椭圆方程;
(2)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,证明:
,|BC|=2|AC|.
(1)建立适当的坐标系,求椭圆方程;
(2)如果椭圆上有两点P、Q,使∠PCQ的平分线垂直于AO,证明: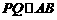 .
.
答案:1. B 2. B 3. A 4. B 5. A 6. B 7. C 8. B 9. D 10. D
17.已知函数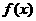 是定义在
是定义在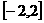 上的奇函数,当
上的奇函数,当 时,
时,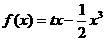 (
(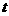 为常数)。
为常数)。
(1)求函数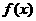 的解析式;
的解析式;
(2)当 时,求
时,求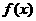 在
在 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的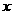 ,并猜想
,并猜想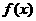 在
在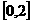 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);
(3)当 时,证明:函数
时,证明:函数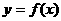 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线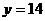 上。
上。

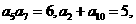 则
则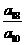 等于
等于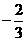 或
或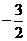 B.
B.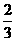 C.
C.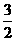 D.
D. 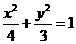 的右焦点到直线
的右焦点到直线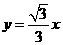 的距离是
的距离是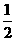 B.
B.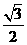 C.1
D.
C.1
D.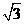
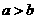 ,则
,则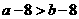 ”的逆否命题是
”的逆否命题是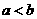 ,则
,则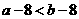 B.若
B.若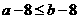 D.若
D.若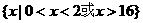
 12.
12.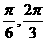 13.
13. 14. 相交 15.
14. 相交 15. 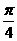
 ,其中
,其中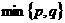 表示
表示 两者中的较小者,
两者中的较小者, 的解为 _____________ 。
的解为 _____________ 。 的函数
的函数 的图象向左平移
的图象向左平移 的一个可能值为 __________ 。
的一个可能值为 __________ 。