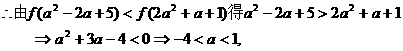1. 已知全集U={a,b,c,d,e,},集合A={b,c},CUB={c,d},则
(CUA) B等于( )
B等于( )
A.{a,e} B。{c,b,d} C。{a.c.e} D 。{e}
22.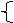 [解](1)h(x)= (-2x+3)(x-2) x∈[1,+∞)
[解](1)h(x)= (-2x+3)(x-2) x∈[1,+∞)
x-2 x∈(-∞,1)
(2) 当x≥1时, h(x)= (-2x+3)(x-2)=-2x2+7x-6=-2(x-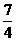 )2+
)2+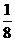
∴h(x)≤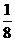 ; 当x<1时, h(x)<-1,
; 当x<1时, h(x)<-1,
∴当x=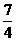 时, h(x)取得最大值是
时, h(x)取得最大值是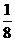
(3)令 f(x)=sinx+cosx,α=
则g(x)=f(x+α)= sin(x+ )+cos(x+
)+cos(x+ )=cosx-sinx,
)=cosx-sinx,
于是h(x)= f(x)·f(x+α)= (sinx+cosx)( cosx-sinx)=cos2x.
另解令f(x)=1+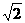 sinx, α=π,
sinx, α=π,
g(x)=f(x+α)=
1+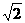 sin(x+π)=1-
sin(x+π)=1-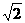 sinx,
sinx,
于是h(x)= f(x)·f(x+α)= (1+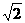 sinx)( 1-
sinx)( 1-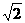 sinx)=cos2x.
sinx)=cos2x.
21.(本小题满分14分)
解: (1) 证明: 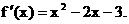 ……………2分
……………2分
假设直线l :  与函数
与函数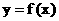 的图像相切, 则
的图像相切, 则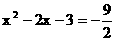 有实数解, 即
有实数解, 即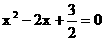 有实数解. ……………5分
有实数解. ……………5分
因为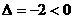 时, 方程
时, 方程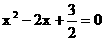 无实数解, 所以直线l与函数
无实数解, 所以直线l与函数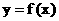 的图像不相切.……………7分
的图像不相切.……………7分
(2) 当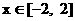 时, 函数
时, 函数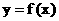 的图像在直线l的下方,
的图像在直线l的下方,
即 对于一切
对于一切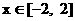 都成立, ……………9分
都成立, ……………9分
即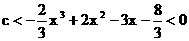 对于一切
对于一切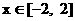 都成立. ……………10分
都成立. ……………10分
令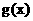
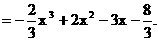 因为
因为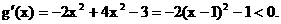
所以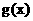 在
在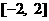 上单调递减, ……………12分
上单调递减, ……………12分
所以当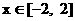 时,
时,  ……………13分
……………13分
所以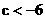 , 所以c的范围是
, 所以c的范围是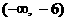 ……………14分
……………14分
22. (本题满分15分)
对定义域分别是Df、Dg的函数y=f(x) 、y=g(x),
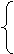 f(x)·g(x) 当x∈Df且x∈Dg
f(x)·g(x) 当x∈Df且x∈Dg
规定: 函数h(x)= f(x)
当x∈Df且x Dg
Dg
g(x) 当x Df且x∈Dg
Df且x∈Dg
(1) 若函数f(x)=-2x+3 ,x≥1; g(x)=x-2,x∈R,写出函数h(x)的解析式;
(2) 求问题(1)中函数h(x)的最大值;
(3) 若g(x)=f(x+α), 其中α是常数,且α∈[0,π],请设计一个定义域为R的函数y=f(x),及一个α的值,使得h(x)=cos2x,并予以证明.
13 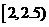 14
14  15 18
15 18
16 582.6元 17 ①②⑤
21.(本小题满分14分)
已知函数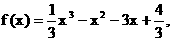 直线l :
直线l :  .
.
(1) 求证: 直线l与函数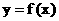 的图像不相切;
的图像不相切;
(2) 若当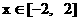 时, 函数
时, 函数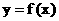 的图像在直线l的下方, 求c的范围.
的图像在直线l的下方, 求c的范围.
20. (本小题共12分) 函数f(x)=x2+ax+3
???(1)当x R时,f(x)≥a恒成立,求a的取值范围
R时,f(x)≥a恒成立,求a的取值范围
(2)当x [-2,2]时, f(x)≥a恒成立,求a的取值范围
[-2,2]时, f(x)≥a恒成立,求a的取值范围

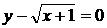 ,x、y
,x、y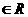 },N={y|
},N={y| x、y
x、y B.
R C. M D. N
B.
R C. M D. N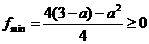 ,
,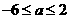 ;
;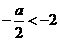 ,
,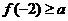 ,不可能;②
,不可能;②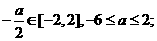
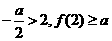 ,
,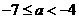
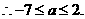
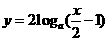
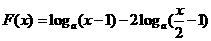 ,(其中
,(其中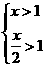 ,即
,即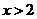 )
) 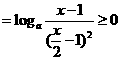
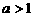 时,
时, 
 时,
时, 
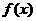 为R上的偶函数,
为R上的偶函数, 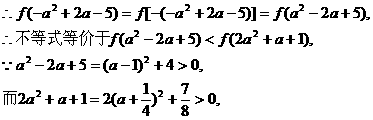
 上单调递增,而偶函数图象关于y轴对称, ∴
上单调递增,而偶函数图象关于y轴对称, ∴