22. [解](1)h(x)=　 (-2x+3)(x-2)　　　 x∈[1,+∞)

　　　　　　　　 x-2　　　　　　 x∈(-∞,1)

　 (2) 当x≥1时, h(x)=　 (-2x+3)(x-2)=-2x²+7x-6=-2(x-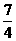)²+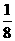

∴h(x)≤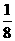;　 当x<1时, h(x)<-1,

∴当x=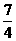时, h(x)取得最大值是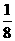

(3)令 f(x)=sinx+cosx,α=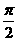

则g(x)=f(x+α)= sin(x+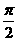)+cos(x+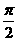)=cosx-sinx,

于是h(x)= f(x)·f(x+α)= (sinx+cosx)( cosx-sinx)=cos2x.

另解令f(x)=1+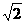sinx, α=π,

g(x)=f(x+α)= 1+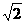sin(x+π)=1-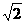sinx,

于是h(x)= f(x)·f(x+α)= (1+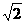sinx)( 1-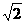sinx)=cos2x.