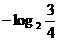19. (本小题共12分)已知F(x)=f(x)-g(x)其中f(x)=loga(x-1),?(a>0,a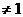 ),且当且仅当点(x0,y0)在f(x)的图象上时,点(2x0,2y0)在
),且当且仅当点(x0,y0)在f(x)的图象上时,点(2x0,2y0)在
y=g(x)的图象上.
(1)求y=g(x)的解析式
(2)当x在什么范围时,F(x)≥0.
18、(本小题共12分) 设f(x)是定义在R上的偶函数,在区间(-∞,0)上单调递增,且满足f(-a2+2a-5)<f(2a2+a+1), 求实数a的取值范围.
设f(x)是定义在R上的偶函数,在区间(-∞,0)上单调递增,且满足f(-a2+2a-5)<f(2a2+a+1), 求实数a的取值范围.
17.?定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在
?[-1,0]上是增函数,则下列正确的是
①f(x)是周期函数 ; ②f(x)的图象关于直线x=1对称 ;
③f(x)在[0,1]上是增函数;④f(x)在[1,2]上是减函数;
⑤f(2)=f(0).
16.某商场宣传在“五一黄金周”期间对顾客购物实行一定的优惠,商场规定:
①如一次性购物不超过200元,不予以折扣;
②如一次性购物超过200元但不超过500元的,按标价给予九折优惠;
③如一次性购物超过500元的,其中500元给予9折优惠,超过500元的部分给予八五折优惠.
某人两次去购物,分别付款176元和432元,如果他只去一次购买同样的商品,则应付款
11.
设f(x)是定义在R上的偶函数,且对任意x都有f(x-1)=f(x+3),在[4,6]上 ,那么在[-2,0]上f(x)的反函数可以表示 ( )
,那么在[-2,0]上f(x)的反函数可以表示 ( )
(A) y=log2(x-4) (B) y=4-log2(x-1)(C) y=4+log2(x-1) (D)y=-log2(x-1)
10. 设f(x)=3ax-2a+1,若存在x0∈(-1,1),使f(x0)=0,则实数a的取值范围是 ( )
(A)
-1<a<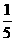 (B) a<-1 (C)
a<-1或a>
(B) a<-1 (C)
a<-1或a> 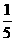 (D) a>
(D) a>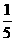

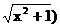 且f(1)=2则f(-1)=
且f(1)=2则f(-1)=
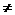 0)在x>0时,f(x)=x-1,则使f(x-1)<0的x的取值范围是
0)在x>0时,f(x)=x-1,则使f(x-1)<0的x的取值范围是 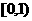 ,则F(x)=f[log0.5(3-x)]的定义域
,则F(x)=f[log0.5(3-x)]的定义域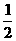 ,则函数u=
,则函数u=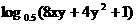 的最大值为( )????(A)
的最大值为( )????(A)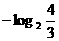 ??(B)0??(C)?1????(D)
??(B)0??(C)?1????(D)