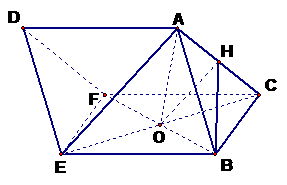
17、(Ⅰ) 证明:∵
证明:∵ 是菱形,
是菱形,
 ∴
∴ 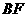 ⊥
⊥ ……………………..1分
……………………..1分
又∵ 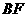 ⊥
⊥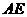 ,且
,且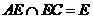
∴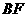 ⊥平面
⊥平面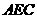 , ……………………..3分
, ……………………..3分
而AO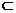 平面
平面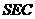
∴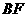 ⊥
⊥
∵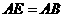 ,
,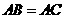 ∴
∴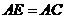
∴ ⊥
⊥ ,且
,且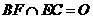
∴ ⊥平面
⊥平面 . ……………5分
. ……………5分
(Ⅱ) 取 的中点
的中点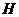 ,连结
,连结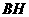 、
、
 ∵
∵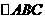 是等边三角形 ∴
是等边三角形 ∴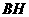 ⊥
⊥
∵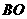 ⊥平面
⊥平面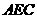 ∴
∴ 是
是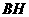 在平面
在平面 上的射影,∴由三垂线定理逆定理 可得
上的射影,∴由三垂线定理逆定理 可得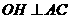
∴ 是二面角
是二面角 的平面角 ……………7分
的平面角 ……………7分
 ≌Rt
≌Rt ,则
,则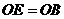 ,∴四边形
,∴四边形 为正方形。
为正方形。
在直角三角形 中,
中,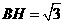 ,
,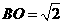 ∴
∴ =
=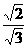 =
=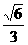 ………9分
………9分
∴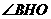 =arcsin
=arcsin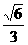 .(或
.(或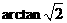 ,
,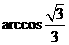 )
)
∴二面角 的大小是arcsin
的大小是arcsin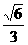 …………………………………10分
…………………………………10分
(Ⅱ)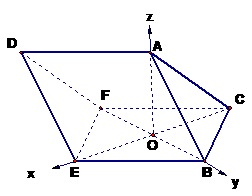 另解:由(Ⅰ)易证
另解:由(Ⅰ)易证 ≌Rt
≌Rt ,则
,则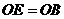 ,
,
∴四边形 为正方形。以
为正方形。以 为原点,
为原点, 所在直线为
所在直线为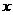 轴,
轴,
FB所在直线为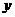 轴, OA所在直线为
轴, OA所在直线为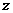 轴,建立空间直角坐标系(如图),则A(0,0,
轴,建立空间直角坐标系(如图),则A(0,0,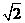 ), B(0,
), B(0, 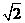 ,0),C(-
,0),C(-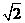 ,0,0),
,0,0),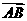 =(0,
=(0,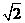 ,-
,-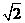 ),
),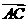 =(-
=(-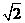 ,0,-
,0,-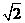 )
)
…………………………………………………………………….7分
设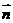 =(
=(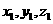 )为平面
)为平面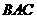 的法向量,则
的法向量,则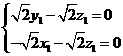
∴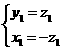 ,取
,取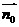 =(-1,1,1)为平面
=(-1,1,1)为平面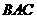 的一个法向量。……………8分
的一个法向量。……………8分
而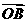 =(0,
=(0, 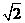 ,0)为平面
,0)为平面 的一个法向量。设
的一个法向量。设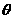 为
为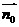 与
与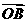 的夹角,则
的夹角,则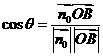 =
=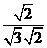 =
=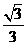 ………………………………………………………….9分
………………………………………………………….9分
∴二面角 的大小为
的大小为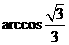 ……………………………………….10分
……………………………………….10分
(Ⅲ)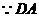 ∥
∥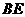 ,
,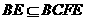

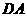 ∥平面
∥平面
∴点 、
、 到面
到面 的距离相等………………………………………………………11分
的距离相等………………………………………………………11分
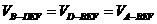 …………………………………………………………………..12分
…………………………………………………………………..12分
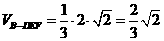 …………………………………………………………14分
…………………………………………………………14分
- 答案

