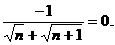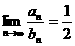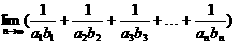19.★(本小题满分10分)已知数列{a_n}、{b_n}都是无穷等差数列,其中a₁=3,b₁=2,b₂是a₂与a₃的等差中项,且.求极限的值.

分析 首先需求出a_n、b_n的表达式,以确定所求极限的表达式,为此,关键在于求出两个数列的公差,“b₂是a₂与a₃的等差中项”已给出一个等量关系,“a_n与b_n之比的极限为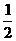”又给出了另一个等量关系,故可考虑先设出公差用二元方程组求解.

解 设{a_n}、{b_n}的公差分别为d₁、d₂,

∵2b₂=a₂+a₃,即2(2+d₂)=(3+d₁)+(3+2d1),

∴2d₂-3d₁=2.①　　 2分

又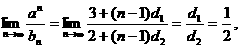

即d₂=2d₁,②　　　 4分

联立①②解得d₁=2,d₂=4.

∴a_n=a₁+(n-1)d₁=3+(n-1)·2=2n+1,

b_n=b₁+(n-1)d₂=2+(n-1)·4=4n-2.　　 6分

10分

18.(本小题满分10分)已知数列{a_n}、{b_n},其中a_n=1+3+5+…+(2n+1),bn=2ⁿ+4(n≥5),试问是否存在这样的自然数n,使得a_n≤b_n成立？

分析 对n赋值后,比较几对a_n与b_n的大小,可作出合理猜测,再用数学归纳法予以证明.

解 a_n=1+3+5+…+(2n+1)=(n+1)²,

当n=5时,a₅=36,b₅=2⁵+4=36,此时a₅=b₅;

当n=6时, a₆=49,b₆=2⁶+4=68,此时a₆<b₆;

当n=7时,a₇=64,b₇=2⁷+4=132,此时a₇<b₇;

当n=8时,a₈=81,b₈=2⁸+4=260,此时a₈<b₈.

猜想:当n≥6时,有a_n<b_n.　　　　 3分

下面用数学归纳法证明上述猜想.

①当n=6时,显然不等式成立,∴n=6时,不等式a_n<b_n成立;

②假设当n=k(k≥6)时,不等式成立,即a_k<b_k,也即(k+1)²<2k+4;当n=k+1时，b_k+1=2^k+1+4=2(2^k+4)-4>2(k+1)²-4=2k²+4k-2,

而(2k²+4k-2)-(k+2)²=k²-6>0(∵k≥6,∴k²＞6),

即2k²+4k-2>(k+2)²=［(k+1)+1］².

由不等式的传递性,知b_k+1>［(k+1)+1］²=a_k+1.

∴当n=k+1时,不等式也成立.　　 8分

由①②可知,对一切n∈N,且n≥6,都有a_n<b_n.

综上所述,可知只有当n=5时,a_n=b_n;当n≥6时,a_n＜b_n.因此存在使a_n≤b_n成立的自然数n.

10分

17.(本小题满分8分)某校有教职工150人,为了丰富教工的课余生活,每天定时开放健身房和娱乐室.据调查统计,每次去健身房的人有10%下次去娱乐室,则在娱乐室的人有20%下次去健身房.请问,随着时间的推移,去健身房的人数能否趋于稳定?

分析 本题考查用数列的递推公式求通项及数列的极限.

解 设第n次去健身房的人数为a_n,去娱乐室的人数为b_n,则a_n+b_n=150,　　　　　　　 2分

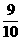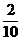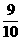∴a_n=a_n-1+b_n-1=a_n-1+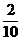(150-a_n-1)=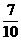a_n-1+30,

即a_n=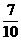a_n-1+30.　　　　　　　　　 4分

∴a_n-100=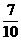(a_n-1-100).于是a_n-100=(a₁-100)·(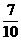)^n-1,即a_n=100+(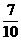)^n-1·(a₁-100).　 6分

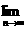∴a_n=100.故随着时间的推移,去健身房的人数稳定在100人左右.　　　　　　　 8分

16.(本小题满分8分)设f(x)是一次函数，f(8)=15,且f(2),f(5),f(4)成等比数列，求.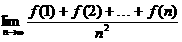

分析 本题为函数、数列、极限的一道综合题.解题关键是先利用待定系数法确定f(x)的解析式，再求f(1)+f(2)+…+f(n),然后利用极限的运算法则求极限.

解 设f(x)=kx+b,

由条件，得8k+b=15,∴b=15-8k.

∵f (2), f (5), f (4)成等比数列,

∴(5k+b)²=(2k+b)(4k+b). 　　　2分

把b=15-8k代入，

得(15-3k)²=(15-6k)(15-4k).

解得k=4,k=0(舍),b=-17.

∴f(x)=4x-17.　　　 4分

∴f(1)+f(2)+…+f(n)

=(4×1-17)+(4×2-17)+…+(4×n-17)

=4×(1+2+…+n)-17n

=4·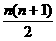-17n=2n²-15n.　　 6分

∴

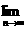
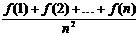
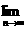
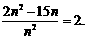=　　　8分

15.(本小题满分8分)平面内有n个圆,其中每两个圆都相交于两点,并且每三个圆都不相交于同一点,求证:n个圆把平面分成f(n)=n²-n+2个部分.

分析 本题的关键在于如何应用归纳假设及已知条件分析当n=k+1时,第k+1个圆与其他k个圆的交点个数,做到有目的的变形.

证明 (1)当n=1时,一个圆把平面分成两部分,又1²-1+2=2,故命题成立.

(2)假设n=k(k∈N*)时,命题成立,即满足题设条件的k个圆把平面分成f(k)=k²-k+2个部分.2分

那么当n=k+1时,设第k+1个圆为⊙O,由题意,它与k个圆中每个圆交于两点,又无三个圆交于同一点,于是它与其他k个圆交于2k个点,这些点把⊙O分成2k条弧,即f(k+1)=f(k)+2k=k²-k+2+2k=(k+1)²-(k+1)+2.　　 6分

这就是说,当n=k+1时,命题也成立.

综上可知,对一切n∈N*,命题都成立.　　 8分

14.已知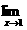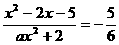,则a的值为　　　　　 .

分析　本题考查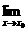f(x)的极限.因为把x=x₀代入分式的分子,分子不为0.又因为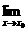f(x)存在,所以把x=x₀代入分母,分母必不为0.故采用直接代入法即可求极限.

解 ∵

答案

13.★设函数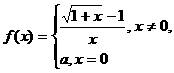在x=0处连续,则实数a的值为　　　　　 .

分析 本题考查函数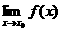的极限及函数f(x)在点x₀处连续的定义.

解 ∵函数f(x)在点x₀处连续,

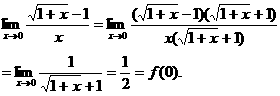
又∵f(0)=a,∴a=.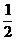

答案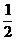

12.()=　　　　　　　　　 .

分析 本题考查数列极限的运算.此题属于“∞-∞”型,应先分子有理化,再求极限.

解 (n-n+1)==

答案 0

11.用数学归纳法证明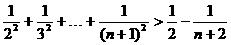,假设n=k时,不等式成立,则当n=k+1时,应推证的目标不等式是　　　　　　　 .

解析 因为自变量取n时,不等式的左边为n项和的形式,所以当n=k+1时应为k+1项的和,它们是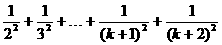,右边只需把n=k+1代入即可,它们是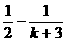,故应推证的不等式是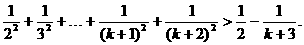

答案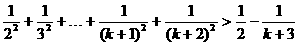

10. 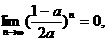则a的取值范围是(　　 )

A.a=1　　　　　　　　　　　　 B.a＜-1或a＞

C.-1＜a＜　　　　　　　　　　 D.a＜-或a＞1

分析 本题考查极限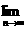qⁿ=0,|q|＜1.要求a的范围,可列a的不等式,要注意分式不等式的解法.

解法一 ∵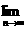(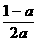)ⁿ=0,∴|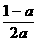|＜1

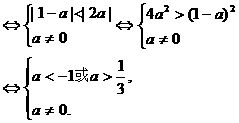
∴a＜-1或a＞.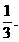

解法二 本题可利用特殊值代入法,当a=1时成立,排除C、D.再令a=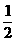,∵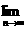(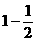)ⁿ=0成立,∴排除A.

答案 B

第Ⅱ卷(非选择题共60分)
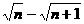