16.(本小题满分8分)设f(x)是一次函数，f(8)=15,且f(2),f(5),f(4)成等比数列，求.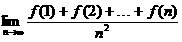

分析 本题为函数、数列、极限的一道综合题.解题关键是先利用待定系数法确定f(x)的解析式，再求f(1)+f(2)+…+f(n),然后利用极限的运算法则求极限.

解 设f(x)=kx+b,

由条件，得8k+b=15,∴b=15-8k.

∵f (2), f (5), f (4)成等比数列,

∴(5k+b)²=(2k+b)(4k+b). 　　　2分

把b=15-8k代入，

得(15-3k)²=(15-6k)(15-4k).

解得k=4,k=0(舍),b=-17.

∴f(x)=4x-17.　　　 4分

∴f(1)+f(2)+…+f(n)

=(4×1-17)+(4×2-17)+…+(4×n-17)

=4×(1+2+…+n)-17n

=4·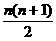-17n=2n²-15n.　　 6分

∴

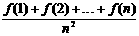
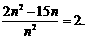=　　　8分