第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1.基本事实(公理):同位角
2.定理1:内错角
定理2:同旁内角
相等
,两直线平行。2.定理1:内错角
相等
,两直线平行。定理2:同旁内角
互补
,两直线平行。
答案:
相等;相等;互补
例1 如图,下列条件能判断$AD// BC$的是 (
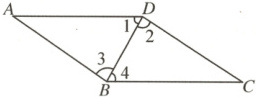
A.$\angle 1=\angle 4$
B.$\angle 1=\angle 2$
C.$\angle 2=\angle 3$
D.$\angle 3=\angle 4$
A
)
A.$\angle 1=\angle 4$
B.$\angle 1=\angle 2$
C.$\angle 2=\angle 3$
D.$\angle 3=\angle 4$
答案:
A
1. 如图,直线$AB$,$CD$分别与直线$MN$交于点$E$,$F$,如果$\angle 1=\angle 2$,那么$AB// CD$,其依据是 (

A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.同位角相等,两直线平行
D
)
A.两直线平行,内错角相等
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.同位角相等,两直线平行
答案:
D
2. 如图,下列能判定$AD// BC$的是 (

A.$\angle ADC + \angle C=180^{\circ}$
B.$\angle ABD = \angle CDB$
C.$\angle ABC + \angle C=180^{\circ}$
D.$\angle ABE = \angle C$
A
)
A.$\angle ADC + \angle C=180^{\circ}$
B.$\angle ABD = \angle CDB$
C.$\angle ABC + \angle C=180^{\circ}$
D.$\angle ABE = \angle C$
答案:
A
例2 如图,台球运动中,如果母球$P$击中边点$A$,经桌边反弹后击中相邻的另一桌边的点$B$,两次反弹。母球$P$经过的路线$BC$与$PA$一定平行吗?请说明理由。

【方法点拨】利用平行线的判定方法解决实际问题时,首先要把实物图抽象为“三线八角”的基本图形,再根据平行线的判定方法进行解题。
解:$BC$与$PA$
理由如下:
$\because \angle PAD=$
$\angle PAB=$
$\therefore \angle PAB=$
同理,$\angle ABC=$
$\because \angle BAE + \angle ABE=$
$\therefore \angle PAB + \angle ABC=$
$\therefore$

【方法点拨】利用平行线的判定方法解决实际问题时,首先要把实物图抽象为“三线八角”的基本图形,再根据平行线的判定方法进行解题。
解:$BC$与$PA$
一定平行
,理由如下:
$\because \angle PAD=$
∠BAE
,$\angle PAB=$
180°-∠PAD-∠BAE
$\therefore \angle PAB=$
180°-2∠BAE
,同理,$\angle ABC=$
180°-2∠ABE
,$\because \angle BAE + \angle ABE=$
90°
,$\therefore \angle PAB + \angle ABC=$
180°
,$\therefore$
PA//BC(同旁内角互补,两直线平行)
。
答案:
一定平行
∠BAE
180°-∠PAD-∠BAE
180°-2∠BAE
180°-2∠ABE
90°
180°
PA//BC(同旁内角互补,两直线平行)
∠BAE
180°-∠PAD-∠BAE
180°-2∠BAE
180°-2∠ABE
90°
180°
PA//BC(同旁内角互补,两直线平行)
3. 我们知道,光线从空气中射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象。如图是光线从空气中射入水中,再从水中射入空气中的示意图。已知$\angle 1 = \angle 2$,$\angle MBC = \angle BCQ$。请你用所学知识判断$AB$与$CD$是否平行,并说明理由。


答案:
AB与CD平行。理由如下:
1.
∵∠MBC=∠BCQ(已知),
∴MN//PQ(内错角相等,两直线平行)。
2.
∵MN//PQ,
∴∠NBC=∠BCP(两直线平行,内错角相等)。
3.
∵∠1=∠2(已知),即∠ABN=∠DCP。
4.
∴∠ABN+∠NBC=∠DCP+∠BCP(等式性质),即∠ABC=∠BCD。
5.
∴AB//CD(内错角相等,两直线平行)。
1.
∵∠MBC=∠BCQ(已知),
∴MN//PQ(内错角相等,两直线平行)。
2.
∵MN//PQ,
∴∠NBC=∠BCP(两直线平行,内错角相等)。
3.
∵∠1=∠2(已知),即∠ABN=∠DCP。
4.
∴∠ABN+∠NBC=∠DCP+∠BCP(等式性质),即∠ABC=∠BCD。
5.
∴AB//CD(内错角相等,两直线平行)。
查看更多完整答案,请扫码查看


