《2026年优课堂给力A加八年级数学上册北师大版》

1. 勾股定理的逆定理：如果三角形的三边长$a$，$b$，$c$满足$a^2 + b^2 = c^2$，那么这个三角形是直角三角形。

答案： $a^2 + b^2 = c^2$

2. 勾股数：满足a² + b² = c²（其中a、b、c为正整数）的三个正整数，称为勾股数。

答案： a² + b² = c²（其中a、b、c为正整数）

例1 如图，已知$\angle ADC = 90°$，$AD = 8$，$CD = 6$，$BC = 24$，$AB = 26$，求图中阴影部分的面积。

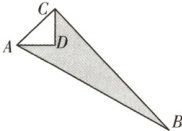
解：在$Rt\triangle ADC$中，
$AC^2 = AD^2 + CD^2$
$ =$$8^2$$+$$6^2$
$=$$100$，
$\therefore AC =$$10$（负值舍去），
在$\triangle ABC$中，$BC = 24$，$AB = 26$，
$\because AC^2 + BC^2 =$$100$$+$$576$，
$AB^2 = 26^2 =$$676$，
$\therefore AC^2 + BC^2 = AB^2$，
$\therefore \triangle ACB$为直角三角形，且$\angle$$ACB$$= 90°$，
$\therefore S_{阴影} = \frac{1}{2}AC · BC - \frac{1}{2}AD · CD$
$ = \frac{1}{2} × 10 × 24 - \frac{1}{2} × 8 × 6 =$$96$，
$\therefore$阴影部分的面积是$96$。

答案： 在$Rt\triangle ADC$中，
$AC^2 = AD^2 + CD^2$
$ = 8^2 + 6^2$
$ = 64 + 36$
$ = 100$，
$\therefore AC = 10$（负值舍去），
在$\triangle ABC$中，$BC = 24$，$AB = 26$，
$\because AC^2 + BC^2 = 100 + 576$，
$AB^2 = 26^2 = 676$，
$\therefore AC^2 + BC^2 = AB^2$，
$\therefore \triangle ACB$为直角三角形，且$\angle ACB = 90°$，
$\therefore S_{阴影} = \frac{1}{2}AC · BC - \frac{1}{2}AD · CD$
$ = \frac{1}{2} × 10 × 24 - \frac{1}{2} × 8 × 6$
$ = 120 - 24$
$ = 96$，
$\therefore$阴影部分的面积是$96$。
答案依次填入为：$8^2$，$6^2$，$100$，$10$，$100$，$576$，$676$，$\angle ACB$，$96$，$96$。

1. 下列各组数中，不能作为直角三角形三边长度的是 （A）

A.$2$，$3$，$4$
B.$3$，$4$，$5$
C.$0.6$，$0.8$，$1$
D.$5$，$12$，$13$

答案： A

2. 三角形的三边$a$，$b$，$c$满足$(a - b)^2 = c^2 - 2ab$，则这个三角形是直角三角形。

答案： 直角

3. 如图1是某品牌婴儿车，图2为其简化结构示意图，现测得$AB = CD = 60 cm$，$BC = 30 cm$，$AD = 90 cm$，其中$AB$与$BD$之间由一个固定为$90°$的零件连接（即$\angle ABD = 90°$），根据安全标准，需满足$BC \perp CD$，通过计算说明该车是否符合安全标准。

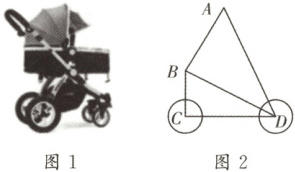
答案： 要判断该车是否符合安全标准，即判断$BC \perp CD$（$\angle BCD = 90°$），步骤如下：
步骤1：在$Rt\triangle ABD$中求$BD$的长度
已知$\angle ABD = 90°$，$AB = 60\, cm$，$AD = 90\, cm$，由勾股定理得：
$AB^2 + BD^2 = AD^2$
代入数值：
$60^2 + BD^2 = 90^2$
$3600 + BD^2 = 8100$
$BD^2 = 8100 - 3600 = 4500$
步骤2：验证$\triangle BCD$是否为直角三角形
在$\triangle BCD$中，已知$BC = 30\, cm$，$CD = 60\, cm$，计算$BC^2 + CD^2$：
$BC^2 + CD^2 = 30^2 + 60^2 = 900 + 3600 = 4500$
由步骤1知$BD^2 = 4500$，因此：
$BC^2 + CD^2 = BD^2$
根据勾股定理的逆定理，$\triangle BCD$为直角三角形，且$\angle BCD = 90°$，即$BC \perp CD$。
结论：该车符合安全标准。

例2 下列各组数中，是勾股数的是（B）
A.$0.3$，$0.4$，$0.5$
B.$3$，$4$，$5$
C.$0.7$，$0.8$，$0.9$
D.$7$，$8$，$9$

答案： B

4. 下面四组数中是勾股数的一组是 （C）

A.$6$，$7$，$8$
B.$1.5$，$2$，$2.5$
C.$21$，$28$，$35$
D.$9$，$16$，$25$

答案： C

5. 能构成一个直角三角形三边长的一组正整数，称为勾股数。请你写出一组都是两位数的勾股数：12,16,20。

答案： 12,16,20