《2026年优课堂给力A加八年级数学上册北师大版》

例 1 如图，有一个圆柱体礼盒，它的高度为$18 cm$，底面周长为$12 cm$。现准备在礼盒表面粘贴彩带作装饰，若彩带的一端粘在$A$处，另一端绕礼盒侧面$2$周后粘贴在$C$处，$B$为$AC$的中点。求至少要准备多长的彩带。

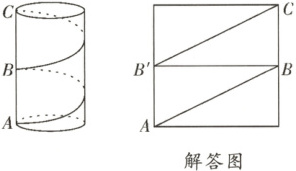
解答图
解：将圆柱的侧面展开如解答图，$AB$和$B'C$即为两圈彩带的最短长度，
则$BC = $12$ cm,BB' = $9$ cm$，
$\therefore B'C^2 = $$BC^2 + BB^{\prime 2}$$ = $225$$，
$\therefore B'C = $_________$ cm$(负值舍去)，
$\therefore$彩带总长为$ $_________$ = $_________$(cm)$。
答：至少要准备____________________$ cm$长的彩带。

答案： 由题可知：圆柱高度为$18$ cm，底面周长为$12$ cm，彩带绕礼盒侧面$2$周。
将圆柱侧面展开成矩形，矩形的高为$18$ cm，宽为$2 × 12=24$cm（绕$2$周）。
点$A$在展开图左下角，点$C$在右上角，彩带绕$2$周，因此$B$为侧面展开后水平方向的中点，即$BB^{\prime} = 18 ÷ 3 × 2 - 1 × 2 ÷ 2 = 9 × 2 ÷ 2 = 9$（cm）（彩带绕$2$周，平分高度为$3$段，每段$9$ cm，$B$为中点，故$BB^{\prime} = 9$ cm）。
$B$为$AC$中点，则$BC=B^{\prime} C$，$BC$水平长度为$12$ cm。
由勾股定理：
$B^{\prime} C^2 = BC^2 + BB^{\prime 2} = 12^2 + 9^2 = 144 + 81 = 225$。
$B^{\prime} C = \sqrt{225} = 15 cm$。
彩带总长为$AB^{\prime} + B^{\prime} C = 15 + 15 = 30$cm。
答：至少要准备$30$ cm长的彩带。
故答案为：$12$；$9$；$BC^2 + BB^{\prime 2}$；$225$；$15$；$AB^{\prime} + B^{\prime} C$；$30$；$30$。

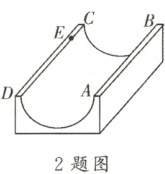
1. 如图，一圆柱高$4 m$，底面周长为$6 m$，小虫在圆柱表面爬行，从下底面上的点$A$处出发，爬到上底面上与点$A$相对的点$B$处，然后再沿另一面爬回$A$点，则小虫爬行的最短路程为10$m$。

答案： 把圆柱侧面展开，其侧面展开图是一个长方形，长为底面圆的周长为$6m$，宽为圆柱的高$4m$。
从下底面上的点$A$处出发，爬到上底面上与点$A$相对的点$B$处，然后再沿另一面爬回$A$点，其最短路径可看作两个相同部分（从$A$到$B$和从$B$到$A$），只需求出从$A$到$B$的最短路径再乘以$2$。
将圆柱展开后，从$A$到$B$的最短路径为直角三角形的斜边，两直角边分别为圆柱的高$4m$和底面周长的一半$3m$。
根据勾股定理$a^2 + b^2 = c^2$（其中$a = 4$，$b = 3$），可得从$A$到$B$的最短路径为：
$\sqrt{4^{2} + 3^{2}}=\sqrt{16 + 9}=\sqrt{25}=5m$。
那么小虫爬行的最短路程为$2×5 = 10m$。
答案为$10$。

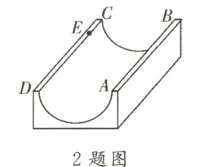
2. 如图是一个滑板场地的 U 型池示意图，可看作是一个长方体去掉一个“半圆柱”而成，中间可滑行部分的截面是弧长为$12 m$的半圆，其边缘$AB = CD = 18 m$，点$E$在$CD$上，且$CE = 2 m$。一位滑板爱好者从点$A$滑到点$E$，那么他滑行的最短距离为20$m$。

答案： 20

3. 如图，透明圆柱形容器（容器厚度忽略不计）的高为$13 cm$，底面周长为$12 cm$，在容器内壁离容器底部$7 cm$的$A$处有一饭粒，此时一只蚂蚁正好在容器外壁且距离容器上沿$2 cm$的点$B$处，求蚂蚁吃到饭粒需爬行的最短路径的长度。

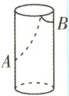
答案： 2√13 cm