第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
1. 勾股定理的验证方法:①测量法;②数格子法;③拼图法(割补法)。
2. 通过面积验证勾股定理的3种常见图形

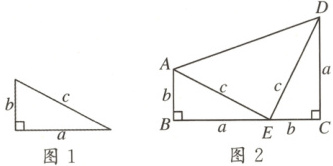
(1)如图1,大正方形的面积可表示为
(2)如图2,大正方形的面积可表示为
(3)如图3,梯形的面积可表示为
2. 通过面积验证勾股定理的3种常见图形

(1)如图1,大正方形的面积可表示为
(a+b)²
或2ab + c²
,据此列等式化简。(2)如图2,大正方形的面积可表示为
c²
或2ab + (a - b)²
,据此列等式化简。(3)如图3,梯形的面积可表示为
(1/2)(a+b)²
或ab + (1/2)c²
,据此列等式化简。
答案:
(1)(a+b)²;2ab + c²
(2)c²;2ab + (a - b)²
(3)(1/2)(a+b)²;ab + (1/2)c²
(1)(a+b)²;2ab + c²
(2)c²;2ab + (a - b)²
(3)(1/2)(a+b)²;ab + (1/2)c²
例1 小颖用四块完全一样的长方形方砖,恰好拼成如图1所示的图案。如图2,连接长方形的对角线后,她发现该图案中可以用“面积法”验证勾股定理。设$AE = a$,$DE = b$,$AD = c$,试说明$a^{2}+b^{2}=c^{2}$。


解:$\because AE = a$,$DE = b$,$AD = c$,
$\therefore S_{ 正方形EFGH}=EH^{2}=$
又$\because S_{ 正方形EFGH}=4S_{\triangle AED}+S_{ 正方形ABCD}$
$=4×$
$\therefore$
化简,得$a^{2}+b^{2}=c^{2}$。


解:$\because AE = a$,$DE = b$,$AD = c$,
$\therefore S_{ 正方形EFGH}=EH^{2}=$
$(a+b)^2$
,又$\because S_{ 正方形EFGH}=4S_{\triangle AED}+S_{ 正方形ABCD}$
$=4×$
$\frac{1}{2}ab$
$+$$c^2$
,$\therefore$
$(a+b)^2$
$=$$2ab + c^2$
,化简,得$a^{2}+b^{2}=c^{2}$。
答案:
$(a+b)^2$;$\frac{1}{2}ab$;$c^2$;$(a+b)^2$;$2ab + c^2$
1. 如图,以图1中的直角三角形为基础,可以构造出以$a$,$b$为底,$(a + b)$为高的直角梯形(如图2),请你利用图2,验证勾股定理。

答案:
梯形面积可以通过两种方式表达:
直接计算梯形面积:
$S = \frac{1}{2} (a + b) × (a + b) = \frac{1}{2}(a + b)^2$。
通过梯形内三个三角形的面积之和表达:
$S = \frac{1}{2}ab + \frac{1}{2}c^2 + \frac{1}{2}ab$。
因为两者表达的是同一个梯形的面积,所以:
$\frac{1}{2}(a + b)^2 = \frac{1}{2}ab + \frac{1}{2}c^2 + \frac{1}{2}ab$,
$\frac{1}{2}(a^2 + 2ab + b^2) = \frac{1}{2}c^2 + ab$,
$a^2 + 2ab + b^2 = c^2 + 2ab$,
$a^2 + b^2 = c^2$。
所以验证了勾股定理:$a^2 + b^2 = c^2$。
直接计算梯形面积:
$S = \frac{1}{2} (a + b) × (a + b) = \frac{1}{2}(a + b)^2$。
通过梯形内三个三角形的面积之和表达:
$S = \frac{1}{2}ab + \frac{1}{2}c^2 + \frac{1}{2}ab$。
因为两者表达的是同一个梯形的面积,所以:
$\frac{1}{2}(a + b)^2 = \frac{1}{2}ab + \frac{1}{2}c^2 + \frac{1}{2}ab$,
$\frac{1}{2}(a^2 + 2ab + b^2) = \frac{1}{2}c^2 + ab$,
$a^2 + 2ab + b^2 = c^2 + 2ab$,
$a^2 + b^2 = c^2$。
所以验证了勾股定理:$a^2 + b^2 = c^2$。
例2 如图,有一盏由传感器$A$控制的灯,装在门上方离地面$4.5\ m$的墙上,任何东西只要移至该传感器周围$5\ m$及$5\ m$以内,灯就会自动发光,一位身高$1.5\ m$的学生要使灯刚好发光,则他与门的距离为
【方法点拨】勾股定理是直角三角形特有的重要定理之一,应用勾股定理需先找出或构造直角三角形。
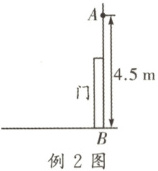
4
$ m$。【方法点拨】勾股定理是直角三角形特有的重要定理之一,应用勾股定理需先找出或构造直角三角形。

答案:
4
2. 如图,直线$AB$是一条高速公路,$C$,$D$是两个村庄,它们到高速公路的距离分别为$AD = 10\ km$,$BC = 15\ km$,且$AB = 25\ km$。现要在$A$,$B$两点之间建一个服务站$E$,使得两个村庄到服务站的距离相等,那么服务站应距离$A$点
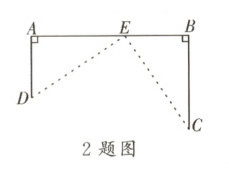
15
$ km$。
答案:
15
查看更多完整答案,请扫码查看


