《2025年三翼单元测试卷黄冈100分六年级数学上册人教版》

2. 计算下面各题，能简便运算的要简便运算。(18分)
$\frac{1}{3} ÷ [\frac{2}{3} - \frac{2}{5}] × \frac{3}{5}$
$(\frac{3}{8} + \frac{5}{6}) × \frac{4}{15}$
$12 × (1 + \frac{1}{3} - \frac{1}{4})$
$1 - \frac{5}{8} - \frac{25}{16} ÷ \frac{3}{10}$
$2.4 × \frac{3}{8} + \frac{1}{10}$
$[\frac{14}{9} × 29 + \frac{58}{9} × 29] × \frac{3}{4}$

答案： 2.$\frac{3}{4}$ $\frac{29}{90}$ 13 $\frac{3}{10}$ 1 174

1. 画一画，涂一涂，分别表示算式的意义或百分数。(6分)

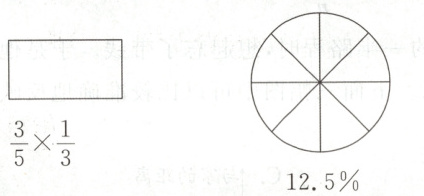
答案：
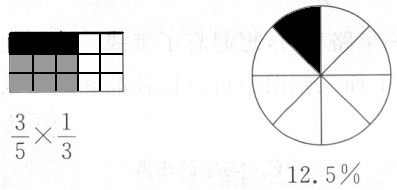
1.

2. 如图，用“十字”分割正方形。分割一次，可以分成4个正方形；分割2次，可以分成7个正方形……用这样的“十字”连续分割3次，可以分成多少个正方形？要分成100个正方形，需要分割多少次？(7分)

答案： 2.解：分割1次，正方形个数：4个；分割2次，正方形个数：4+3=7(个)；分割3次，正方形个数：4+3+3=10(个)。由此规律可得，分割n次，正方形个数：4+3(n - 1)=(3n + 1)个。当正方形有100个时，3n + 1=100，解得n=33。

1. 玲玲的存钱罐里有18枚一元硬币，一元硬币的数量是五角硬币的$\frac{2}{3}$，一角硬币的数量比五角硬币多$\frac{4}{9}$。玲玲的存钱罐里一共有多少钱？(5分)

答案： 1.18÷$\frac{2}{3}$=27(枚) 0.5×27=13.5(元) 27×(1 + $\frac{4}{9}$)=39(枚) 0.1×39=3.9(元) 18 + 13.5 + 3.9=35.4(元)