《2025年天利38套高中名校期中期末联考测试卷高中数学必修第一册人教版》

1. 已知集合 $ A = \{ 2,0,3 \} $，$ B = \{ 2,3 \} $，则(D)

A.$ A = B $
B.$ A \cap B = \varnothing $
C.$ A \subsetneqq B $
D.$ B \subsetneqq A $

答案： 1.D集合相等+集合的交集运算+集合的包含关系　因为集合$A=\{2,0,3\},B=\{2,3\}$，所以$A\neq B$，$A\cap B=\{2,3\}$，$B\subsetneqq A$，所以A，B，C错误，D正确，故选D.

2. 设 $ a,b,c \in \mathbf{R} $，且 $ a ＞ b $，则下列结论正确的是(C)

A.$ a ^ { 2 } ＞ b ^ { 2 } $
B.$ \frac { 1 } { a } ＜ \frac { 1 } { b } $
C.$ 2 ^ { a } ＞ 2 ^ { b } $
D.$ a c ^ { 2 } ＞ b c ^ { 2 } $

答案： 2.C不等式的性质　对于A，若$a=0,b=-1$，则$a^{2}＜b^{2}$，故A不正确；对于B，若$a=1,b=-1$，则$\frac{1}{a}＞\frac{1}{b}$，故B不正确；对于C，由于$y=2^{x}$在R上单调递增，$a＞b$，则$2^{a}＞2^{b}$，故C正确；对于D，若$c=0$，则$ac^{2}=bc^{2}$，故D错误，故选C.

3. 已知函数 $ f ( x ) = ( x + a - 2 ) ( 2 x ^ { 2 } + a - 1 ) $为奇函数，则 $ a $ 的值是(B)

A.1
B.2
C.1 或 2
D.0

答案： 3.B奇函数的性质及应用
　解法一:因为函数$f(x)=(x+a-2)(2x^{2}+a-1)$为奇函数，定义域为$(-\infty,+\infty)$，所以$f(0)=(a-2)(a-1)=0$(题眼)，解得$a=1$或$a=2$，当$a=1$时，$f(x)=2x^{2}(x-1)$，则$f(-x)=2x^{2}(-x-1)\neq -f(x)$，不满足题意；当$a=2$时，$f(x)=x(2x^{2}+1)$，则$f(-x)=-x(2x^{2}+1)=-f(x)$，满足题意，所以$a$的值是2，故选B.
　解法二:验证法,当$a=1$时，$f(x)=2x^{2}(x-1)=2x^{3}-2x^{2}$，$f(-x)=-2x^{3}-2x^{2}\neq -f(x)$，所以排除A和C；当$a=0$时，$f(x)=(x-2)(2x^{2}-1)=2x^{3}-4x^{2}-x+2$，$f(-x)=-2x^{3}-4x^{2}+x+2\neq -f(x)$，所以排除D，故选B.

4. “$ \log _ { 2 } x ＜ 2 $”是“$ 1 ＜ x ＜ 3 $”的(B)

A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件

答案： 4.B充分条件与必要条件的判断　由$\log_{2}x＜2=\log_{2}4$，解得$0＜x＜4$(题眼).因为$\{x\mid1＜x＜3\}$是$\{x\mid0＜x＜4\}$的真子集，所以“$\log_{2}x＜2$”是“$1＜x＜3$”的必要不充分条件，故选B.

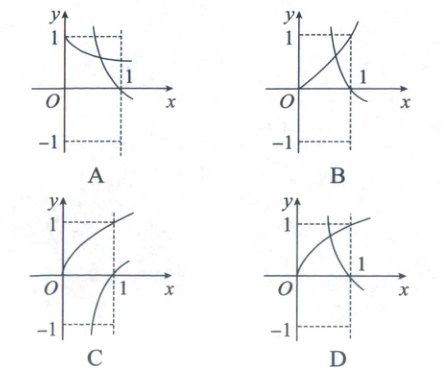
5. 在同一直角坐标系中，函数 $ f ( x ) = x ^ { a } ( x \geq 0 ) $，$ g ( x ) = \log _ { a } x $ 的图象可能是(D)

答案： 5.D幂函数与对数函数的图象　对于A，没有幂函数的图象，不符合题意；对于B，$y=x^{a}(x\geqslant0)$中$a＞1$，$y=\log_{a}x(x＞0)$中$0＜a＜1$，不符合题意；对于C，$y=x^{a}(x\geqslant0)$中$0＜a＜1$，$y=\log_{a}x(x＞0)$中$a＞1$，不符合题意；对于D，$y=x^{a}(x\geqslant0)$中$0＜a＜1$，$y=\log_{a}x(x＞0)$中$0＜a＜1$，符合题意，故选D.

6. “学如逆水行舟，不进则退；心似平原跑马，易放难收”（明·《增广贤文》）是勉励人们专心学习的。如果每天的“进步”率都是 $ 1 \% $，那么一年后是 $ ( 1 + 1 \% ) ^ { 365 } = 1.01 ^ { 365 } $；如果每天的“退步”率都是 $ 1 \% $，那么一年后是 $ ( 1 - 1 \% ) ^ { 365 } = 0.99 ^ { 365 } $。一年后“进步”的是“退步”的 $ \frac { 1.01 ^ { 365 } } { 0.99 ^ { 365 } } = ( \frac { 1.01 } { 0.99 } ) ^ { 365 } \approx 1481 $倍。如果甲、乙两人目前水平相当，接下来甲每天的“进步”率和乙每天的“退步”率都是 $ 20 \% $，那么大约经过（ ）天后甲的水平约为乙的一万倍。（$ \lg 2 \approx 0.3010 $，$ \lg 3 \approx 0.4771 $）

A.20
B.21
C.22
D.23

答案： 6.D对数运算　设经过$x$天后甲的水平约为乙的$10000$倍，则$\frac{(1+20\%)^{x}}{(1-20\%)^{x}}=10000$，即$(\frac{1.2}{0.8})^{x}=10000$，$\therefore x=\log_{\frac{3}{2}}10000=\frac{\lg10000}{\lg\frac{3}{2}}=\frac{4}{\lg3-\lg2}\approx\frac{4}{0.1761}\approx23$，故选D.

7. 已知 $ a = 0.9 ^ { \frac { 1 } { 3 } } $，$ b = ( \frac { 1 } { 3 } ) ^ { 0.9 } $，$ c = \frac { 1 } { 2 } \log _ { 27 } 9 $，则(D)

A.$ a ＜ c ＜ b $
B.$ b ＜ c ＜ a $
C.$ b ＜ a ＜ c $
D.$ c ＜ b ＜ a $

答案： 7.D指数函数的单调性+对数的运算　由题意得，$c=\frac{1}{2}\log_{27}9=\frac{1}{2}\log_{3}3^{2}=\frac{1}{2}×\frac{2}{3}=\frac{1}{3}$.因为$y=(\frac{1}{3})^{x}$在R上单调递减(题眼)，所以$(\frac{1}{3})^{1}＜(\frac{1}{3})^{a}＜(\frac{1}{3})^{0.5}$，又$(\frac{1}{3})^{0.5}=\frac{\sqrt{3}}{3}\approx0.7$；因为$y=0.9^{x}$在R上单调递减，所以$a=0.9^{\frac{1}{9}}＞0.9^{1}=0.9$，所以$c＜b＜a$，故选D.

8. 已知定义域为 $ ( 0, + \infty ) $的函数 $ f ( x ) $满足对于任意 $ x _ { 1 }, x _ { 2 } \in ( 0, + \infty ) $，$ x _ { 1 } \neq x _ { 2 } $，都有 $ \frac { x _ { 1 } f ( x _ { 2 } ) - x _ { 2 } f ( x _ { 1 } ) } { x _ { 2 } - x _ { 1 } } ＞ 1 $，且 $ f ( 3 ) = 2 $，则不等式 $ f ( x ) ＜ x - 1 $的解集为(C)

A.$ ( - \infty, 2 ) $
B.$ ( 0, 2 ) $
C.$ ( 0, 3 ) $
D.$ ( 2, 3 ) $

答案： 8.C函数的单调性
[思维导图]$\frac{x_{1}f(x_{2})-x_{2}f(x_{1})}{x_{2}-x_{1}}＞1$等价变形
$\begin{cases}\frac{[f(x_{2})+1]x_{2}-[f(x_{1})+1]x_{1}}{x_{2}-x_{1}}＞0\\令0＜x_{1}＜x_{2}\end{cases}$
$\frac{f(x_{2})+1}{x_{2}}-\frac{f(x_{1})+1}{x_{1}}=\frac{[f(x_{2})+1]x_{1}-[f(x_{1})+1]x_{2}}{x_{1}x_{2}}$构造函数$g(x)=\frac{f(x)+1}{x}(x＞0)$
研究$g(x)$的单调性得解.
由$\frac{x_{1}f(x_{2})-x_{2}f(x_{1})}{x_{2}-x_{1}}＞1$，得$\frac{x_{1}f(x_{2})-x_{2}f(x_{1})}{x_{2}-x_{1}}-1＞0$，即$\frac{x_{1}x_{2}[f(x_{2})+1]-x_{2}x_{1}[f(x_{1})+1]}{x_{2}-x_{1}}＞0$(题眼)，令$0＜x_{1}＜x_{2}$，则$x_{2}-x_{1}＞0$，$x_{1}x_{2}＞0$，得$\frac{f(x_{2})+1}{x_{2}}-\frac{f(x_{1})+1}{x_{1}}＞0$，(关键：等价变形，合理同构)，设$g(x)=\frac{f(x)+1}{x}(x＞0)$，则$g(x_{1})＜g(x_{2})$，所以函数$g(x)$在$(0,+\infty)$上单调递增，且$g(3)=\frac{f(3)+1}{3}=1$，则$f(x)＜x - 1$，即$\frac{f(x)+1}{x}＜1$，即$g(x)＜g(3)$，故$0＜x＜3$，即不等式$f(x)＜x - 1$的解集为$(0,3)$，故选C.

9. 下列说法中正确的有(BC)

A.命题 $ p : \exists x \in \mathbf { R } $，$ x ^ { 2 } + 2 x + 2 ＜ 0 $，则命题 $ p $的否定是 $ \forall x \in \mathbf { R } $，$ x ^ { 2 } + 2 x + 2 ＞ 0 $
B.“$ m ＜ 0 $”是“关于 $ x $ 的方程 $ x ^ { 2 } - 2 x + m = 0 $有一正一负根”的充要条件
C.奇函数 $ f ( x ) $和偶函数 $ g ( x ) $的定义域都是 $ \mathbf { R } $，则函数 $ h ( x ) = f ( g ( x ) ) $为偶函数
D.“$ \sqrt { x } ＞ \sqrt { y } $”是“$ x ＞ y $”的必要条件

答案： 9.BC存在量词命题的否定+函数奇偶性的判断+充分条件与必要条件的判断　对于A，命题$p:\exists x\in\mathbf{R},x^{2}+2x + 2＜0$，则命题$p$的否定是$\forall x\in\mathbf{R},x^{2}+2x + 2\geqslant0$，故A错误；对于B，当$m＜0$时，对于方程$x^{2}-2x + m=0$有$\Delta=4 - 4m＞0$，所以方程有两个不等实根，设为$x_{1},x_{2}$，则$x_{1}x_{2}=m＜0$，即$x_{1}$，$x_{2}$一正一负，故充分性成立；当$x^{2}-2x + m=0$有一正一负根时，只需满足$x_{1}x_{2}＜0$，即$m＜0$，故必要性成立，即“$m＜0$”是“关于$x$的方程$x^{2}-2x + m=0$有一正一负根”的充要条件，故B正确；对于C，由题意知$h(x)$的定义域为$\mathbf{R}$，由$f(-x)=-f(x)$，$g(-x)=g(x)$，可得$h(-x)=f(g(-x))=f(g(x))=h(x)$，即函数$h(x)=f(g(x))$为偶函数，故C正确；对于D，当$\sqrt{x}＞\sqrt{y}$时，可得$x＞y\geqslant0$，反之，当$x＞y$，比如$0＞x＞y$时，$\sqrt{x}$，$\sqrt{y}$无意义，故“$\sqrt{x}＞\sqrt{y}$”是“$x＞y$”的充分条件，故D错误，故选BC.