《2025年天利38套高中名校期中期末联考测试卷高中数学必修第一册人教版》

10. 已知 $ f(x) $ 是定义在 $ \mathbf{R} $ 上且不恒为 0 的函数，则下列选项正确的是(ABD)

A.$ f(x) - f(-x) $ 为奇函数
B.若 $ f(x) $ 是奇函数，则 $ y = |f(x)| $ 为偶函数
C.若 $ y = |f(x)| $ 为偶函数，则 $ f(x) $ 是奇函数
D.若 $ f(x) $ 为偶函数，则 $ f(f(x)) $ 为偶函数

答案： 10. ABD 函数的奇偶性 对于 A,令$F(x)=f(x)-f(-x)$,$F(x)$的定义域为$\mathbf{R}$,则$F(-x)=f(-x)-f(x)=-[f(x)-f(-x)]=-F(x)$,所以$f(x)-f(-x)$为奇函数,所以 A 正确;对于 B,因为$f(x)$为奇函数,所以$f(-x)=-f(x)$,所以$\vert f(-x)\vert=\vert -f(x)\vert=\vert f(x)\vert$,所以$y=\vert f(x)\vert$是偶函数,所以 B 正确;对于 C,令$f(x)=\cos x$,易判断函数$y=\vert\cos x\vert$是偶函数,显然$f(x)=\cos x$不是奇函数,所以 C 错误;对于 D,因为$f(x)$为偶函数,所以$f(-x)=f(x)$,所以$f(f(-x))=f(f(x))$,则$f(f(x))$为偶函数,所以 D 正确,故选 ABD.

11. 已知 $ a $，$ b $，$ c $ 均为正实数，则下列选项正确的是(BC)

A.若 $ \frac{2}{a} + 3b = 2 $，则 $ \frac{b}{a} \geq \frac{1}{6} $
B.若 $ a(a + b + c) + bc = 1 $，则 $ 2a + b + c \geq 2 $
C.若 $ \frac{2}{a} + 3b = 2 $，则 $ \frac{a}{a + 1} + \frac{2}{3b} ＞ 2 $
D.若 $ 2a + b + c = 2 $，则 $ a(a + b + c) + bc \geq 1 $

答案： 11. BC 基本不等式的应用
【思维导图】对于 A,直接应用基本不等式判断最值;对于 B,构造基本不等式判断最值;对于 C,利用含$a$的式子表示$b$,利用不等式的性质判断最值;对于 D,构造基本不等式判断最值.
对于 A,$\frac{2}{a}+3b=2\geq2\sqrt{\frac{6b}{a}}$(提示:直接应用基本不等式),所以$\frac{b}{a}\leq\frac{1}{6}$,所以 A 错误;对于 B,因为$a(a + b + c)+bc = 1$,即$(a + b)(a + c)=1$(关键:将已知条件转化为因式乘积的形式,便于应用基本不等式判断最值),所以由$(a + b)(a + c)\leq(\frac{a + b + a + c}{2})^{2}$(提示:基本不等式)可知,$2a + b + c\geq2$,所以 B 正确;对于 C,因为$\frac{2}{a}+3b=2$,所以$3b=2-\frac{2}{a}$,又$b＞0$,所以$2-\frac{2}{a}＞0$,解得$a＞1$,此时有$\frac{a}{a + 1}+\frac{2}{3b}=\frac{a}{a + 1}+\frac{a}{a + 1 - a^{2}}=\frac{2a^{2}}{a^{2}-1}=2+\frac{2}{a^{2}-1}＞2$,所以 C 正确;对于 D,$2a + b + c=2=(a + b)+(a + c)\geq2\sqrt{(a + b)(a + c)}$,所以$(a + b)·(a + c)\leq1$,即$a(a + b + c)+bc\leq1$,所以 D 错误,故选 BC.

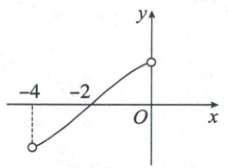
12. 已知 $ f(x) $ 是定义在区间 $ (-4, 4) $ 上的奇函数，$ f(x) $ 的部分图象如图所示，则关于 $ x $ 的不等式 $ f(x) ＜ 0 $ 的解集是$(-4,-2)\cup(0,2)$。

答案： 12. $(-4,-2)\cup(0,2)$ 函数的基本性质+不等式的解法
结合图象可知当$-4＜x＜-2$时,$f(x)＜0$;当$-2＜x＜0$时,$f(x)＞0$,由奇函数的对称性可知当$0＜x＜2$时,$f(x)＜0$;当$2＜x＜4$时,$f(x)＞0$(提示:奇函数的图象关于原点对称),所以$f(x)＜0$的解集为$(-4,-2)\cup(0,2)$.

13. 经科学家研究，地震时释放出的能量 $ E $(单位：焦耳)与地震里氏震级 $ M $ 之间的关系为 $ \lg E = 4.8 + 1.5M $。2011 年，某海域发生里氏 9.0 级地震，它所释放出来的能量是 2008 年 5 月 12 日我国汶川发生里氏 8.0 级地震的$10\sqrt{10}$倍。

答案： 13. $10\sqrt{10}$ 对数运算 由题可得,$\lg E_{1}=4.8 + 1.5×9,\lg E_{2}=4.8+1.5×8$,所以$\lg E_{1}-\lg E_{2}=\lg\frac{E_{1}}{E_{2}}=1.5$,即$\frac{E_{1}}{E_{2}}=10^{1.5}=10\sqrt{10}$,所以是$10\sqrt{10}$倍.

14. 已知函数 $ f(x) = \begin{cases} x^2 + 2, & 0 ＜ x \leq 2 \\ 2x^2 - x, & x ＞ 2 \end{cases} $，若函数 $ h(x) = f(x) - ax $ 有两个不同的零点 $ x_1 $，$ x_2 $，且 $ 1 ＜ x_2 - x_1 ＜ 2 $，则实数 $ a $ 的取值范围是$(3,\sqrt{17})$。

答案： 14. $(3,\sqrt{17})$ 分段函数的图象+函数的零点
【思维导图】已知条件$\rightarrow$函数$y=\frac{f(x)}{x}$的图象与直线$y = a$有两个交点,其横坐标分别为$x_{1},x_{2}\rightarrow$当$x+\frac{2}{x}=3$时,$x_{1}=1,x_{2}=2$不满足题意$\rightarrow a=x_{1}+\frac{2}{x_{1}}=2x_{2}-1\rightarrow$用$a$表示$x_{2}-x_{1}\rightarrow$建立不等式组$\rightarrow$得解.
函数$h(x)=f(x)-ax$有两个不同的零点$x_{1},x_{2}$,即$f(x)=ax$有两个解$x_{1},x_{2}$,也就是函数$y=\frac{f(x)}{x}=\begin{cases}x+\frac{2}{x},0＜x\leq2\\2x - 1,x＞2\end{cases}$的图象与直线$y = a$有两个交点,其横坐标分别为$x_{1},x_{2}$,因为当$x+\frac{2}{x}=3$时,两根分别为$1,2$,所以不满足题意,所以$a=x_{1}+\frac{2}{x_{1}}=2x_{2}-1$,所以$x_{1}=\frac{a - \sqrt{a^{2}-8}}{2},x_{2}=\frac{a + 1}{2}$(关键:用$a$表示$x_{1},x_{2}$).因为$1\leq x_{2}-x_{1}＜2$(题眼),所以$1＜\frac{1 + \sqrt{a^{2}-8}}{2}＜2$,即有$1＜a^{2}-8＜9$,所以$9＜a^{2}＜17$,解得$3＜a＜\sqrt{17}$.

15. (13 分)
已知集合 $ A = \{ x | x^2 - 6x + 8 \geq 0 \} $，$ B = \{ x | m - 3 \leq x \leq m + 1 \} $。
(Ⅰ) 当 $ m = 2 $ 时，求 $ A \cap B $；
(Ⅱ) 问题：已知① $ A \cup (\complement_{\mathbf{R}} B) = \mathbf{R} $，② $ A \cup B = A $，③ $ B \cap (\complement_{\mathbf{R}} A) = \varnothing $，求实数 $ m $ 的取值范围。
在① $ A \cup (\complement_{\mathbf{R}} B) = \mathbf{R} $，② $ A \cup B = A $，③ $ B \cap (\complement_{\mathbf{R}} A) = \varnothing $ 这三个条件中任选一个，补充在上面的问题中，并进行解答。
注：如果选择多个条件分别解答，按第一个解答计分。

答案： 15. (Ⅰ)$\{x\mid - 1\leq x\leq2\}$ (Ⅱ)$\{m\mid m\leq1$或$m\geq7\}$ 集合的运算
解:(Ⅰ)由条件得,$A=\{x\mid x\leq2$或$x\geq4\}$(提示:一元二次不等式的解法),当$m = 2$时,$B=\{x\mid - 1\leq x\leq3\}$,此时$A\cap B=\{x\mid - 1\leq x\leq2\}$.
(Ⅱ)条件①,②,③均可以得到$B\subseteq A$(题眼),所以$m + 1\leq2$或$m - 3\geq4$,解得$m\leq1$或$m\geq7$,故实数$m$的取值范围是$\{m\mid m\leq1$或$m\geq7\}$. (13 分)