1. 下列运算正确的是(
A.$a^{5}\cdot a^{3}= a^{15}$
B.$6a^{2m}÷ 2a^{m}= 3a^{2}$
C.$(-a^{5})^{2}= a^{10}$
D.$a^{6}÷ a^{3}= a^{2}$
C
)A.$a^{5}\cdot a^{3}= a^{15}$
B.$6a^{2m}÷ 2a^{m}= 3a^{2}$
C.$(-a^{5})^{2}= a^{10}$
D.$a^{6}÷ a^{3}= a^{2}$
答案:
C
2. 把代数式$x^{2}y - 4y$分解因式,下列结果正确的是(
A.$y(x + 2)(x - 2)$
B.$y(x + 4)(x - 4)$
C.$y(x^{2}-4)$
D.$y(x - 2)^{2}$
A
)A.$y(x + 2)(x - 2)$
B.$y(x + 4)(x - 4)$
C.$y(x^{2}-4)$
D.$y(x - 2)^{2}$
答案:
A
3. 下列四个算式:①$(2x - 1)^{2}= 4x^{2}-2x + 1$;②$(-2m - n)(2m + n)= 4m^{2}-n^{2}$;③$(a + 3b)^{2}= a^{2}+6ab + 9b^{2}$;④$(-x + 2y)(x + 2y)= 4y^{2}-x^{2}$.其中正确的个数是(
A.1个
B.2个
C.3个
D.4个
B
)A.1个
B.2个
C.3个
D.4个
答案:
B
4. 按下列程序计算,最后输出的答案是(

$\boxed{a}\to\boxed{立方}\to\boxed{-a}\to\boxed{÷ a}\to\boxed{+1}\to\boxed{答案}$
A.$a^{3}$
B.$a^{2}+1$
C.$a^{2}$
D.$a$
C
)
$\boxed{a}\to\boxed{立方}\to\boxed{-a}\to\boxed{÷ a}\to\boxed{+1}\to\boxed{答案}$
A.$a^{3}$
B.$a^{2}+1$
C.$a^{2}$
D.$a$
答案:
C
5. 已知$a + b = 2$,则$a^{2}-b^{2}+4b$的值是(
A.2
B.3
C.4
D.6
C
)A.2
B.3
C.4
D.6
答案:
C
6. 如果$x^{2}-6x + k^{2}$恰好是另一个整式的平方,那么常数$k$的值为(
A.9
B.3
C.-3
D.$\pm 3$
D
)A.9
B.3
C.-3
D.$\pm 3$
答案:
D
7. 已知$x + y = -5$,$xy = 6$,则$x^{2}+y^{2}$的值是(
A.1
B.13
C.17
D.25
B
)A.1
B.13
C.17
D.25
答案:
B
8. 已知$a^{m}= 2$,$a^{n}= 3$,则$a^{m + 2n}$的值为(
A.11
B.18
C.38
D.12
B
)A.11
B.18
C.38
D.12
答案:
B
9. 计算几何图形的积可表示一些代数恒等式,如图1可表示的代数恒等式是(
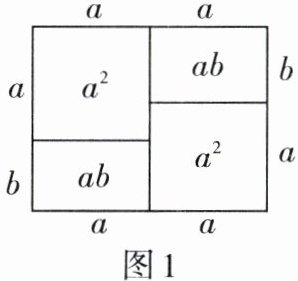
A.$(a - b)^{2}= a^{2}-2ab + b^{2}$
B.$(a + b)^{2}= a^{2}+2ab + b^{2}$
C.$2a(a + b)= 2a^{2}+2ab$
D.$(a + b)(a - b)= a^{2}-b^{2}$
C
)
A.$(a - b)^{2}= a^{2}-2ab + b^{2}$
B.$(a + b)^{2}= a^{2}+2ab + b^{2}$
C.$2a(a + b)= 2a^{2}+2ab$
D.$(a + b)(a - b)= a^{2}-b^{2}$
答案:
C
10. 若$(y^{2}+ay)(y^{2}-3y - 9b)的结果中不含y^{2}和y^{3}$项,则$ab$的值为(
A.$\frac{1}{3}$
B.3
C.$-\frac{1}{3}$
D.-3
D
)A.$\frac{1}{3}$
B.3
C.$-\frac{1}{3}$
D.-3
答案:
D
查看更多完整答案,请扫码查看


