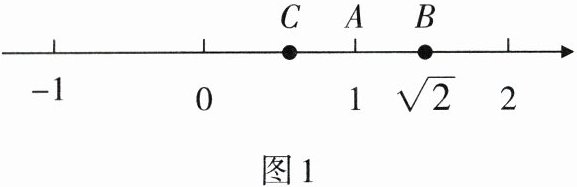
10. 如图1,数轴上表示$1,\sqrt{2}的对应点分别为A,B$,点$B关于点A的\underset{\cdot }{$
A.$2-\sqrt{2}$
B.$\sqrt{2}-2$
C.$\sqrt{2}-1$
D.$1-\sqrt{2}$
对
$}\underset{\cdot }{$称
$}\underset{\cdot }{$点
$}为C$,则点$C$所表示的数是(A
)
A.$2-\sqrt{2}$
B.$\sqrt{2}-2$
C.$\sqrt{2}-1$
D.$1-\sqrt{2}$
答案:
A
1. 如果某数的一个平方根是$-5$,那么这个数为
25
.
答案:
25
2. $6\dfrac{1}{4}$的算术平方根是
$\frac{5}{2}$
,$-3\dfrac{3}{8}$的立方根是$-\frac{3}{2}$
.
答案:
$\frac{5}{2},-\frac{3}{2}$
3. $2-\sqrt{5}$的相反数是
$\sqrt{5}-2$
,$2-\sqrt{5}$的绝对值是$\sqrt{5}-2$
.
答案:
$\sqrt{5}-2,\sqrt{5}-2$
4. $5x + 12的立方根是3$,则$x$的值是
3
.
答案:
3
1. 计算:
(1)$\pm \sqrt{\dfrac{25}{169}}$;
(2)$\sqrt[3]{\dfrac{37}{64}-1}$;
(3)$10-\sqrt{121}$;
(4)$\sqrt[3]{8}+\sqrt{0}-\sqrt{\dfrac{1}{9}}$.
(1)$\pm \sqrt{\dfrac{25}{169}}$;
(2)$\sqrt[3]{\dfrac{37}{64}-1}$;
(3)$10-\sqrt{121}$;
(4)$\sqrt[3]{8}+\sqrt{0}-\sqrt{\dfrac{1}{9}}$.
答案:
(1)$\pm \frac{5}{13}$;(2)$-\frac{3}{4}$;(3)$-1$;(4)$1\frac{2}{3}$
查看更多完整答案,请扫码查看


