《2025年新课程课堂同步练习册八年级数学上册华师大版》

1. 在Rt△ABC中,∠C= 90°,AB∶BC= 5∶3,AC= 16,求AB,BC的长.

答案： $AB=20,BC=12$

2. 如图7是由边长为1 m的正方形地砖铺设的地面示意图,求小明沿图中所示的折线A→B→C所走的路程(结果保留根号).

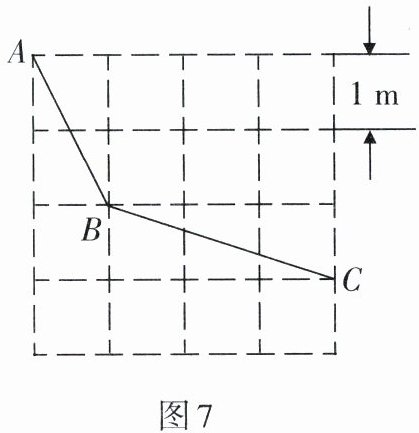
答案： $(\sqrt{5}+\sqrt{10})\ m$

3. 如图8,△AOB,△COD是等腰直角三角形,点D在AB上.
(1)求证：△AOC≌△BOD；
(2)若AD= 3,BD= 1,求CD的长.

答案： 1. （1）证明：
因为$\triangle AOB$，$\triangle COD$是等腰直角三角形，所以$OA = OB$，$OC = OD$，$\angle AOB=\angle COD = 90^{\circ}$。
则$\angle AOB-\angle AOD=\angle COD-\angle AOD$，即$\angle AOC=\angle BOD$。
在$\triangle AOC$和$\triangle BOD$中，$\begin{cases}OA = OB\\\angle AOC=\angle BOD\\OC = OD\end{cases}$。
根据$SAS$（边角边）定理，可得$\triangle AOC\cong\triangle BOD$。
2. （2）
因为$\triangle AOC\cong\triangle BOD$，所以$AC = BD = 1$，$\angle CAO=\angle B$。
又因为$\triangle AOB$是等腰直角三角形，所以$\angle OAB=\angle B = 45^{\circ}$，则$\angle CAO = 45^{\circ}$。
所以$\angle CAD=\angle CAO+\angle OAB=45^{\circ}+45^{\circ}=90^{\circ}$。
在$Rt\triangle CAD$中，根据勾股定理$CD=\sqrt{AC^{2}+AD^{2}}$。
已知$AD = 3$，$AC = 1$，则$CD=\sqrt{1^{2}+3^{2}}=\sqrt{1 + 9}=\sqrt{10}$。
综上，（1）已证$\triangle AOC\cong\triangle BOD$；（2）$CD$的长为$\sqrt{10}$。