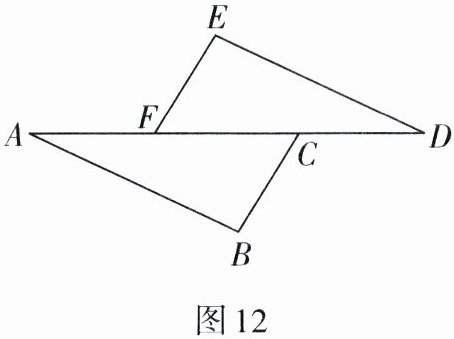
1. 如图 12,$ AF = DC $,$ BC // EF $,请只补充一个条件,使得 $ \triangle ABC \cong \triangle DEF $,并说明理由。

答案:
提示:可补充EF=BC或∠E=∠B或∠A=∠D
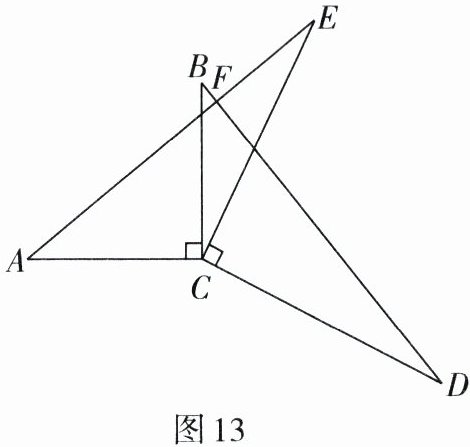
2. 如图 13,$ AC \perp BC $,$ DC \perp EC $,$ AC = BC $,$ DC = EC $,$ AE $ 与 $ BD $ 交于点 $ F $。
(1) 求证:$ AE = BD $;
(2) 求 $ \angle AFD $ 的度数。
(1) 求证:$ AE = BD $;
(2) 求 $ \angle AFD $ 的度数。

答案:
1. (1)证明$AE = BD$:
因为$AC\perp BC$,$DC\perp EC$,所以$\angle ACB=\angle DCE = 90^{\circ}$。
那么$\angle ACB+\angle BCE=\angle DCE+\angle BCE$,即$\angle ACE=\angle BCD$。
在$\triangle ACE$和$\triangle BCD$中:
已知$AC = BC$,$\angle ACE=\angle BCD$,$DC = EC$。
根据全等三角形判定定理($SAS$:两边及其夹角对应相等的三角形全等),可得$\triangle ACE\cong\triangle BCD$。
由全等三角形的性质(全等三角形对应边相等),所以$AE = BD$。
2. (2)求$\angle AFD$的度数:
设$AC$与$BD$交于点$G$。
因为$\triangle ACE\cong\triangle BCD$,所以$\angle A=\angle B$。
在$\triangle AGF$和$\triangle BGC$中,$\angle AGF=\angle BGC$(对顶角相等)。
根据三角形内角和定理$\angle A+\angle AGF+\angle AFD = 180^{\circ}$,$\angle B+\angle BGC+\angle BCA = 180^{\circ}$。
又因为$\angle A=\angle B$,$\angle AGF=\angle BGC$,所以$\angle AFD=\angle BCA$。
已知$\angle BCA = 90^{\circ}$,所以$\angle AFD = 90^{\circ}$。
综上,(1)已证$AE = BD$;(2)$\angle AFD$的度数为$90^{\circ}$。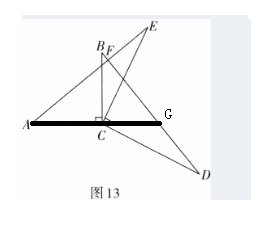
1. (1)证明$AE = BD$:
因为$AC\perp BC$,$DC\perp EC$,所以$\angle ACB=\angle DCE = 90^{\circ}$。
那么$\angle ACB+\angle BCE=\angle DCE+\angle BCE$,即$\angle ACE=\angle BCD$。
在$\triangle ACE$和$\triangle BCD$中:
已知$AC = BC$,$\angle ACE=\angle BCD$,$DC = EC$。
根据全等三角形判定定理($SAS$:两边及其夹角对应相等的三角形全等),可得$\triangle ACE\cong\triangle BCD$。
由全等三角形的性质(全等三角形对应边相等),所以$AE = BD$。
2. (2)求$\angle AFD$的度数:
设$AC$与$BD$交于点$G$。
因为$\triangle ACE\cong\triangle BCD$,所以$\angle A=\angle B$。
在$\triangle AGF$和$\triangle BGC$中,$\angle AGF=\angle BGC$(对顶角相等)。
根据三角形内角和定理$\angle A+\angle AGF+\angle AFD = 180^{\circ}$,$\angle B+\angle BGC+\angle BCA = 180^{\circ}$。
又因为$\angle A=\angle B$,$\angle AGF=\angle BGC$,所以$\angle AFD=\angle BCA$。
已知$\angle BCA = 90^{\circ}$,所以$\angle AFD = 90^{\circ}$。
综上,(1)已证$AE = BD$;(2)$\angle AFD$的度数为$90^{\circ}$。

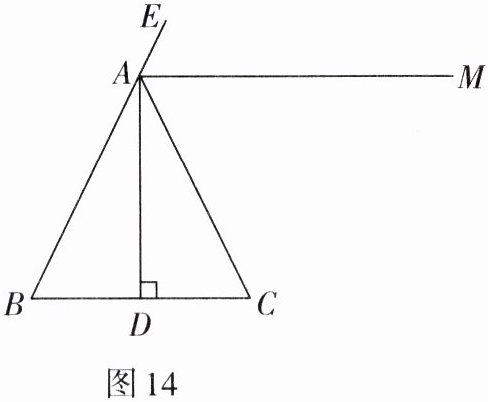
3. 如图 14,在 $ \triangle ABC $ 中,$ AB = AC $,$ AD $ 是高,$ AM $ 是 $ \triangle ABC $ 外角 $ \angle CAE $ 的平分线。
(1) 用尺规作图方法,作 $ \angle ADC $ 的平分线 $ DN $,交 $ AC $ 于点 $ N $(保留作图痕迹,不写作法和证明);
(2) 设 $ DN $ 与 $ AM $ 交于点 $ F $,判断 $ \triangle ADF $ 的形状,并加以证明。
(1) 用尺规作图方法,作 $ \angle ADC $ 的平分线 $ DN $,交 $ AC $ 于点 $ N $(保留作图痕迹,不写作法和证明);
(2) 设 $ DN $ 与 $ AM $ 交于点 $ F $,判断 $ \triangle ADF $ 的形状,并加以证明。

答案:
(1)略
(2)在△ABC中
∵AB=AC,AD是高
∴AD平分∠BAC 又AM平分∠CAE
∴AD⊥AM
∵AD是高,DN平分∠ADC,交AM于F
∴∠ADF=45°
∴∠AFD=45°
∴AD=AF 即△ADF是等腰直角三角形
(1)略
(2)在△ABC中
∵AB=AC,AD是高
∴AD平分∠BAC 又AM平分∠CAE
∴AD⊥AM
∵AD是高,DN平分∠ADC,交AM于F
∴∠ADF=45°
∴∠AFD=45°
∴AD=AF 即△ADF是等腰直角三角形
查看更多完整答案,请扫码查看


