8. 现有两根木棒,长度分别为40 cm和41 cm. 若要钉成一个三角形木架,其中有一个角为直角,所需最短的木棒长度是(
A.8 cm
B.9 cm
C.10 cm
D.11 cm
B
)A.8 cm
B.9 cm
C.10 cm
D.11 cm
答案:
B
9. 如图2,某自动感应门的正上方A处装着一个感应器,该感应器离地的距离AB= 2.5 m,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高为1.6 m的学生CD正对门,走到离门1.2 m的地方时(BC= 1.2 m),感应门自动打开,则该学生的头顶离感应器的距离AD等于(
A.1.2 m
B.1.5 m
C.2.0 m
D.2.5 m
B
)
A.1.2 m
B.1.5 m
C.2.0 m
D.2.5 m
答案:
B
10. 如图3,已知长方形ABCD中,AB= 3 cm,AD= 9 cm,将此长方形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为(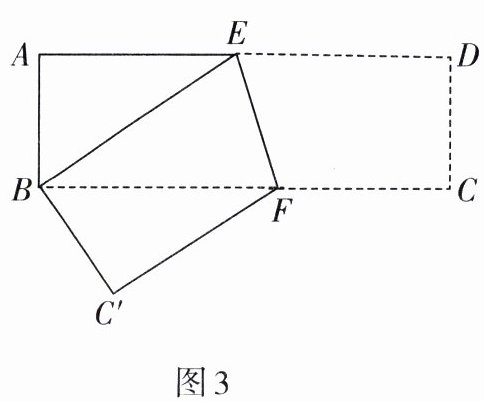
$A.6 cm^2$
$B.8 cm^2$
$C.10 cm^2$
$D.12 cm^2$
A
)
$A.6 cm^2$
$B.8 cm^2$
$C.10 cm^2$
$D.12 cm^2$
答案:
A
1. 用反证法证明“在△ABC中,如果AB= c,BC= a,AC= b,且∠C≠90°,那么$a^{2}+b^{2}≠c^{2}$”的第一步是
假设$a^{2}+b^{2}=c^{2}$
.
答案:
假设$a^{2}+b^{2}=c^{2}$
2. 如图4,以直角三角形DEF的三边为边向外作正方形A,B,C,若正方形B的面积为100,正方形C的面积为36,则图中正方形A的面积是
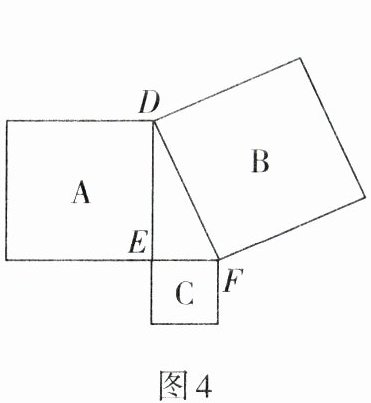
64
.
答案:
64
3. 如图5,在矩形ABCD中,AD= 3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE= EF,则AB的长为
$\sqrt{18}$
.
答案:
$\sqrt{18}$
4. 如图6,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为
$\sqrt{27}$
.
答案:
$\sqrt{27}$
查看更多完整答案,请扫码查看


