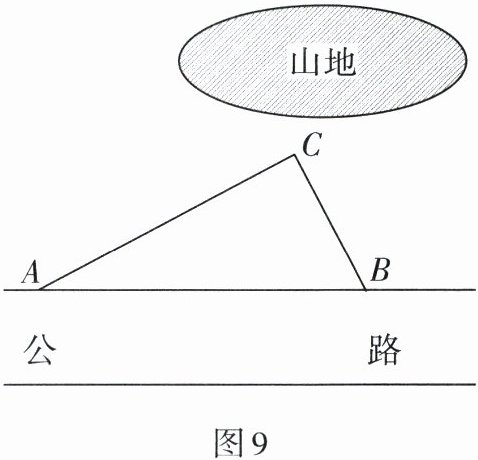
4. 如图9,在甲村至乙村的公路旁有一块山地正在开发,现有一C处需要爆破,已知点C与公路上的停靠站A的距离为400米,与公路上的停靠站B的距离为300米,且CA⊥BC. 为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB段是否因有危险而需要暂时封锁?

答案:
因为C点到AB的距离为240米,所以道路必须封锁
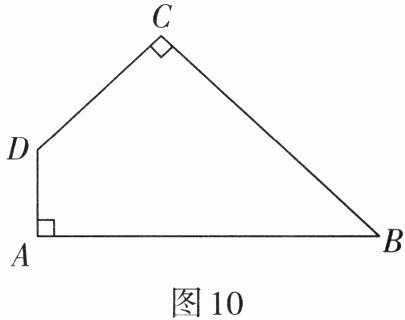
5. 如图10,四边形ABCD中, ∠A= ∠C= 90°,∠B= 45°,AD= 1,AB= 4,试求四边形ABCD的面积.

答案:
$\frac{23}{4}$
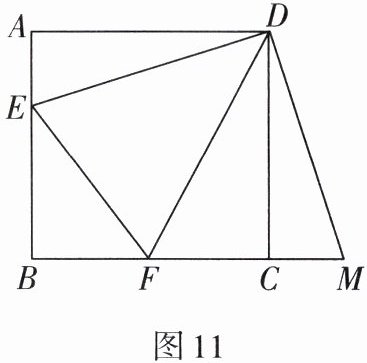
6. 如图11,已知正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且∠EDF= 45°,将△DAE绕点D按逆时针方向旋转90°得到△DCM.
(1)求证:EF= MF;
(2)当AE= 1时,求EF的长.
(1)求证:EF= MF;
(2)当AE= 1时,求EF的长.

答案:
(1)提示:利用SAS证明$\triangle DEF\cong\triangle DMF$,由全等三角形的对应边相等可得出$EF=MF$
(2)$\frac{5}{2}$ 提示:设$EF=MF=x$,可得出$BF=BM-MF=4-x$,在$Rt\triangle BEF$中,利用勾股定理列出方程$2^{2}+(4-x)^{2}=x^{2}$,求出方程的解得到x的值,即为EF的长
(1)提示:利用SAS证明$\triangle DEF\cong\triangle DMF$,由全等三角形的对应边相等可得出$EF=MF$
(2)$\frac{5}{2}$ 提示:设$EF=MF=x$,可得出$BF=BM-MF=4-x$,在$Rt\triangle BEF$中,利用勾股定理列出方程$2^{2}+(4-x)^{2}=x^{2}$,求出方程的解得到x的值,即为EF的长
查看更多完整答案,请扫码查看


